本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/database/106504.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
GAN对抗生成网络(二)——算法及Python实现
1 算法步骤
上一篇提到的GAN的最优化问题是,本文记录如何求解这一问题。
首先为了表示方便,记,这里让最大的可视作常量。
第一步,给定初始的,使用梯度上升找到 ,最大化。关于梯度下降,可以参考笔者另一篇…
深入理解Java中的Set集合:特性、用法与常见操作指南
一、HashSet集合
1.HashSet集合的特点 2.HashSet常用方法
①:add(Object o):向Set集合中添加元素,不允许添加重复数据。
②:size():返回Set集合中的元素个数
③.remove(Object o): 删除Set集合中的obj对…
oceanbase集群访问异常问题处理
1.报错现象 2.问题排查
检查obproxy状态发现为不可用状态 重启obproxy 依次重启Obproxy集群 观察任务状态 重启完成 Obproxy状态正常 3.验证登录
登录成功
CSS 学习之 padding 与图形绘制
padding 属性和 background-clip 属性配合,可以在有限的标签下实现一些 CSS 图形绘制效果,我这里举两个小例子,重在展示可行性。
例 1:不使用伪元素,仅一层标签实现大队长的“三道杠”分类图标效果。此效果在移动端比较常见&…
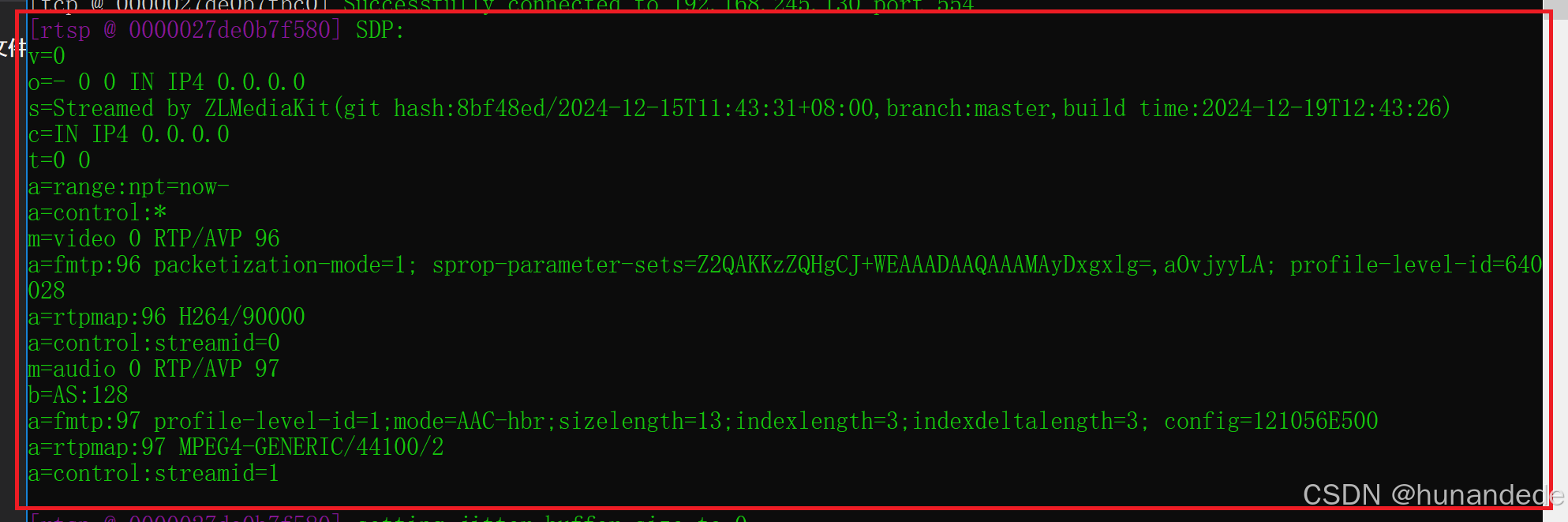
FFmpeg 4.3 音视频-多路H265监控录放C++开发二十一.4,SDP协议分析
SDP在4566 中有详细描述。 SDP 全称是 Session Description Protocol, 翻译过来就是描述会话的协议。 主要用于两个会话实体之间的媒体协商。 什么叫会话呢,比如一次网络电话、一次电话会议、一次视频聊天,这些都可以称之为一次会话。 那为什…
25年1月更新。Windows 上搭建 Python 开发环境:Python + PyCharm 安装全攻略(文中有安装包不用官网下载)
引言 随着 Python 在数据科学、Web 开发、自动化脚本等多个领域的广泛应用,越来越多的开发者选择它作为首选编程语言。而 PyCharm 作为一个功能强大的集成开发环境(IDE),为 Python 开发者提供了极大的便利。本文将详细介绍如何在 …
UE蓝图战利品掉落动画
战利品掉落动画,其实就是添加个冲量 add impulse
什么是冲量?
冲量 (impulse)是作用在物体上的力 在 时间上的累积效果
树莓派之旅-第一天 系统的烧录和设置
自言自语: 在此记录一下树莓派的玩法。以后有钱了买点来玩啊草
系统的安装烧录
系统下载
树莓派官网:https://www.raspberrypi.com/ 首页点击SoftWare进入OS下载页面 这里是安装工具:安装工具负责将系统镜像安装到sd卡中 点击下载符合自己…
QT:控件属性及常用控件(1)------核心控件及属性
一个图形化界面上的内容,不需要我们直接从零去实现 QT中已经提供了很多的内置控件: 按钮,文本框,单选按钮,复选按钮,下拉框等等。。。。。 文章目录 1.常用控件属性1.1 enabled1.2 geometry1.2.1 geometry…
汽车驾校转型做无人机执照培训详解, “驾” 起无人机培训新未来?
汽车驾校转型做无人机执照培训,这一趋势确实在一定程度上预示着无人机培训领域的新未来。以下是对这一转型的详细分析:
一、转型背景 1. 无人机行业快速发展:
无人机技术在农业、影视、安防、物流等多个领域的应用不断拓展,市场…
C语言----指针数组
目录
1. 定义:
2. 格式:
应用示例
1) 用于存放普通变量的地址
2) 用于存放二维数组的每一行第一个元素的地址(列地址)
3) 用于存放字符串
4) 命令行参数
补充:开辟堆区空间(动态空间开辟࿰…
免费下载 | 2025年中国智慧园区行业发展白皮书
《2025年中国智慧园区行业发展白皮书》的核心内容包括以下几个方面: 智慧园区概述: 定义:智慧园区是结合物联网、云计算、大数据、人工智能等技术,具备互联互通、开放共享、协同运作、创新发展的新型园区模式。分类:依…
深入刨析数据结构之排序(上)
目录
1.内部排序
1.1概述
1.2插入排序
1.2.1其他插入排序
1.2.1.1 折半插入排序
1.2.1.2 2-路插入排序
1.3希尔排序
1.4快速排序
1.4.1起泡排序
1.4.2快速排序
1.4.2.1hoare版本
1.4.2.2挖坑版本
1.4.2.3前后指针版本
1.4.2.4优化版本
1.4.2.4.1小区间插入排序优…
机器学习 学习知识点
机器学习 学习知识点 什么是消融实验(Ablation experiment)?num_step与batch_size的区别python glob.glob()函数认识python的条件判断之is not、is not None、is Nonetqdm介绍及常用方法softmax 激活函数。type_as(tesnor)Python OpenCV cv2.…
CSS 中 content换行符实现打点 loading 正在加载中的效果
我们动态加载页面内容的时候,经常会使用“正在加载中…”这几个字,基本上,后面的 3 个点都是静态的。静态的问题在于,如果网络不流畅,加载时间比较长,就会给人有假死的 感觉,但是,如…
Anaconda3-2024 下载与安装教程
文章目录 简介(一)软件概述(二)主要功能(三)应用场景 一、下载(一)官网下载(二)网盘分享 二、安装 简介 (一)软件概述
集成环境 Anac…
京存助力人工大模型训练
随着人工智能技术的迅猛发展,深度学习模型变得越来越复杂,训练所需的数据量也日益庞大。在这个背景下,数据的存储与处理成为了一个至关重要的环节。京存存储,作为一家专注于高性能存储解决方案的公司,凭借其卓越的产品…
第2章波动光学引论—抓本质,本质必定简单
1波动光学的电磁理论
1.1波动方程
1)波动方程是通过描述波函数随时间和空间的变化来表达波动的传播和演化。
2)一维波动方程: a.一维波动方程描述了沿着一条直线传播的波动。它的一般形式为: ∂u/∂t v ∂u/∂x 其中ÿ…
Qt窗口获取Tftpd32_svc服务下载信息
前言 一个由Qt开发的Windows小工具需要布置Tftp协议服务端来支持设备下载数据,并显示下载列表(进度、下载源等)。 考虑开发方便,优先使用了Qtftp方案,经测试发现,不够稳定,会有下载超时的情况&a…