本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/database/121730.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Create Deploy Your Website Quickly - Docusaurus GitHub Pages
文章目录 1. 简介2. 准备3. 创建项目4. 问题4.1 GIT_USERGhostwritten yarn deploy 卡住 1. 简介
Docusaurus 是一个开源框架,用于快速构建、部署和托管技术文档。它支持 Markdown 格式,提供了主题和插件,支持版本控制,适合开发者…
『大模型笔记』Ollama环境变量大全!
『大模型笔记』Ollama环境变量大全! 文章目录 一. Ollama环境变量大全!1. 命令方式查看2. 源码整理二. 参考文献一. Ollama环境变量大全!
1. 命令方式查看 Ollama常用的环境变量ollama help serve2. 源码整理 从源代码中整理了这份文档,希望有缘人能发现它。变量默认值说明…
DeepSeek本地化部署【window下安装】【linux下安装】
一、window 本地安装指导
1.1、下载window安装包
https://ollama.com/download/OllamaSetup.exe
1.2、点击下载好的安装包进行安装
检测安装是否成功:
C:\Users\admin>ollama -v
ollama version is 0.5.7有上面的输出,则证明已经安装成功。
配置…
【快速幂算法】快速幂算法讲解及C语言实现(递归实现和非递归实现,附代码)
快速幂算法
快速幂算法可用分治法实现
不难看出,对任意实数a和非负整数n,有: a n { 1 , n 0 , a ≠ 0 0 , a 0 ( a n 2 ) 2 , n > 0 , n 为偶数 ( a n 2 ) 2 ∗ a , n > 0 , n 为奇数 a^n \begin{cases} 1, & n 0, a\neq 0…
华为支付-商户基础支付场景准备
一、场景介绍 例如用户出行需要提前预定酒店房间,此时用户可打开商户开发的APP应用/元服务,选好预定房间后发起支付,商户通过接入华为支付拉起华为支付收银台完成单个订单支付。 支持商户模型:直连商户、平台类商户、服务商 华为支…
高并发场景下,如何用无锁实现高性能LRU缓存?
《百万人高并发场景下,我如何用无锁实现高性能LRU缓存?》
LRU算法核心原理
LRU(Least Recently Used)算法是缓存系统的核心淘汰策略,其核心逻辑可以用一张流程图描述:
(图:访问数…
【C++】C++-教师信息管理系统(含源码+数据文件)【独一无二】
👉博__主👈:米码收割机 👉技__能👈:C/Python语言 👉专__注👈:专注主流机器人、人工智能等相关领域的开发、测试技术。 【C】C教师信息管理系统(含源码&#x…
基于SpringBoot的电影院售票管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI、Python、小程序等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、Vue项目源码、SSM项目源码、微信小程序源码 精品专栏:…
elementui: el-dialog的header设置样式不生效
问:
el-dialog的header设置样式不生效
回答:
场景: <el-dialogv-model"dialogVisible"width"800px":before-close"beforeClose"append-to-body:close-on-click-modal"false"title"增加文…
STM32 ADC介绍(硬件原理篇)
目录
背景
AD转换器
采样与保持
量化
编码
AD转换器转换原理
DA转换原理
AD转换原理 背景
在数字系统的广泛应用中,用数字系统处理模拟量的情况十分普遍,因此引入了模拟信号和数字信号的接口问题。为了解决这一问题,首先利用模数转换…
逻辑回归不能解决非线性问题,而svm可以解决
逻辑回归和支持向量机(SVM)是两种常用的分类算法,它们在处理数据时有一些不同的特点,特别是在面对非线性问题时。
1. 逻辑回归
逻辑回归本质上是一个线性分类模型。它的目的是寻找一个最适合数据的直线(或超平面&…
多媒体软件安全与授权新范例,用 CodeMeter 实现安全、高效的软件许可管理
背景概述
Reason Studios 成立于 1994 年,总部位于瑞典斯德哥尔摩,是全球领先的音乐制作软件开发商。凭借创新的软件产品和行业标准技术,如 ReWire 和 REX 文件格式,Reason Studios 为全球专业音乐人和业余爱好者提供了一系列高质…
DeepSeek 突然来袭,AI 大模型变革的危机与转机藏在哪?
随着人工智能技术的飞速发展,大模型领域不断涌现出具有创新性的成果。DeepSeek 的横空出世,为 AI 大模型领域带来了新的变革浪潮。本文将深入探讨 DeepSeek 出现后 AI 大模型面临的危机与转机。
冲冲冲!!! 目录
一、…
【蓝桥杯嵌入式】8_IIC通信-eeprom读写
全部代码网盘自取 链接:https://pan.baidu.com/s/1PX2NCQxnADxYBQx5CsOgPA?pwd3ii2 提取码:3ii2 1、电路图 这个电路允许通过I2C总线与EEPROM(M24C02-WMN6TP)和数字电位器(MCP4017T-104ELT)进行通信。EEPROM用于存储数据,而数字电位器可以用…
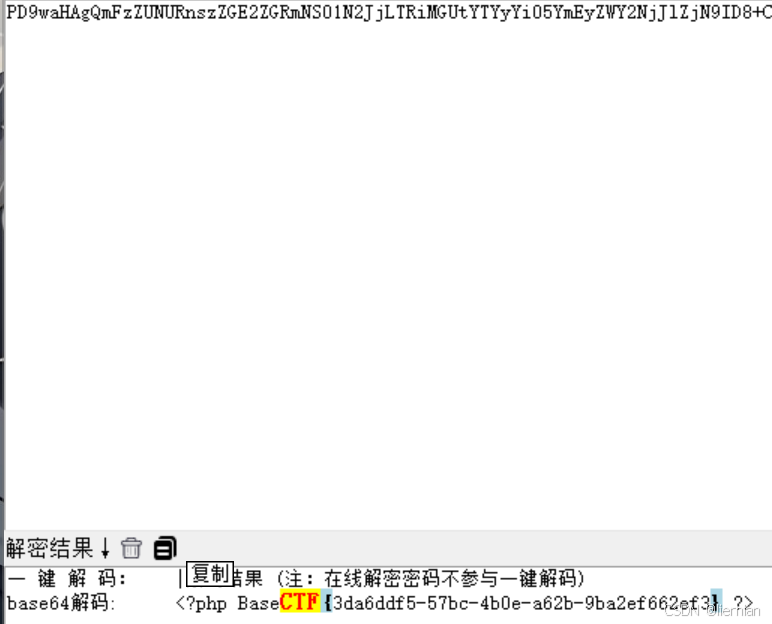
2024BaseCTF_week4_web上
继续!冲冲冲
目录
圣钥之战1.0 nodejs 原型 原型链 原型链污染 回到题目
flag直接读取不就行了? 圣钥之战1.0 from flask import Flask,request
import jsonapp Flask(__name__)def merge(src, dst):for k, v in src.items():if hasattr(dst, __geti…
树莓集团与宜宾“双轮驱动“共启新程 数字经济集群落子川南
2 月 13 日的宜宾市翠屏区招商引资签约活动,见证了树莓集团与宜宾的深度合作。双方以 “双轮驱动” 模式,共启新的发展征程。 树莓集团将在翠屏区实施 “数字产业化 产业数字化” 双轮驱动。数字产业化方面,集团将投入资源,打造具…
linux系统测试网络pps、带宽和延时(方案来源于阿里云)
此方案来源于阿里云
pps测试
步骤
分别在测试机和辅助测试机上执行以下命令,下载Netperf。
wget https://benchmark-packages.oss-cn-qingdao.aliyuncs.com/netperf-2.7.0.tar.gz分别在测试机和辅助测试机上执行以下命令,安装Netperf和sar监控工具。…
hive高频写入小数据,导致hdfs小文件过多,出现查询效率很低的情况
问题描述
hive高频写入小数据,导致hdfs小文件过多,出现查询效率很低的情况分析过程
先复现现象
select count() from ads.ads_sdd_flow_managemlt_to_ids_mm;–15分钟,小文件10983 select max(mm) from ads.ads_sdd_flow_managemlt_to_ids…
进阶数据结构——树状数组
前言
看这篇文章前我建议你们先看这个视频还有这个视频,不然你们可能看不懂。
一、树状数组的核心思想与本质
核心思想:树状数组(Fenwick Tree)是一种用于高效处理前缀和查询和单点更新的数据结构。 本质:通过二进…