本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/database/71936.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
【JavaEE】——回显服务器的实现
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录
一:引入
1:基本概念
二:UDP socket API使用
1:socke…
决策树(descision tree)
一:决策树的基础介绍
决策树(descision tree)是一种基本的分类与回归的方法。决策树是一种对实例进行预测的树型结构。
下面是一个完整的二叉决策树,根据西瓜的几个特征判断西瓜的好坏。
纹理<1.5代表第一个判断条件,根据纹理<1.5是…
2024年9月国产数据库大事记-墨天轮
本文为墨天轮社区整理的2024年9月国产数据库大事件和重要产品发布消息。
目录
2024年9月国产数据库大事记 TOP102024年9月国产数据库大事记(时间线)产品/版本发布兼容认证代表厂商大事记厂商活动相关资料
2024年9月国产数据库大事记 TOP10 2024年9月国…
传奇GOM引擎架设好进游戏后提示请关闭非法外挂,重新登录,如何处理?
今天在架设一个GOM引擎的版本时,进游戏之后刚开始是弹出一个对话框,提示请关闭非法外挂,重新登录,我用的是绿盟登陆器,同时用的也是绿盟插件,刚开始我以为是绿盟登录器的问题,于是就换成原版gom…
年薪30W的Java程序员都要求熟悉JVM与性能调优!
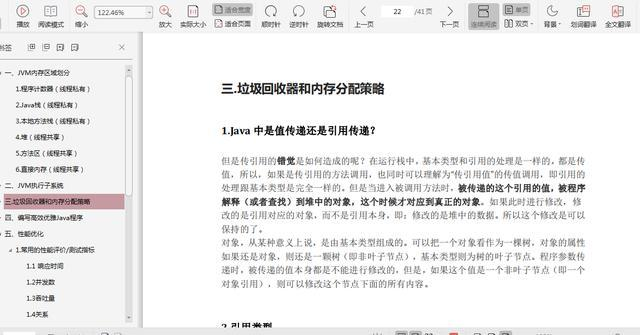
一、JVM 内存区域划分
1.程序计数器(线程私有)
程序计数器(Program Counter Register),也有称作为 PC 寄存器。保存的是程序当前执行的指令的地址(也可以说保存下一条指令的所在存储单元的地址࿰…
IDM6.42下载器最新版本,提速你的网络生活!
🚀【速度与激情,IDM 6.42来袭!】💣 Hey, 亲爱的下载达人们!👋 今天我要给你们安利一个神器——Internet Download Manager(简称IDM),版本6.42,这可不是普通的…
【docker】要将容器中的 livox_to_pointcloud2 文件夹复制到宿主机上
复制文件夹 使用 docker cp 命令从容器复制文件夹到宿主机:
docker cp <container_id_or_name>:/ws_livox/src/livox_to_pointcloud2 /path/to/host/folder sudo docker cp dandong_orin_docker:/ws_livox/src/livox_to_pointcloud2 /home
【redis-06】redis的stream流实现消息中间件
redis系列整体栏目 内容链接地址【一】redis基本数据类型和使用场景https://zhenghuisheng.blog.csdn.net/article/details/142406325【二】redis的持久化机制和原理https://zhenghuisheng.blog.csdn.net/article/details/142441756【三】redis缓存穿透、缓存击穿、缓存雪崩htt…
DBMS-3.4 SQL(4)——存储过程和函数触发器
本文章的素材与知识来自李国良老师和王珊老师。 存储过程和函数 一.存储过程
1.语法 2.示例
(1) 使用DELIMITER更换终止符后用于编写存储过程语句后,在下次执行SQL语句时记得再使用DELIMITER将终止符再换回分号。
使用DELIMITER更换终止符…
《企业实战分享 · SonarQube10.x 代码质量推广手册》
📢 大家好,我是 【战神刘玉栋】,有10多年的研发经验,致力于前后端技术栈的知识沉淀和传播。 💗 🌻 CSDN入驻不久,希望大家多多支持,后续会继续提升文章质量,绝不滥竽充数…
字符集、字符串的创建以及操作
字符集 字符串的创建
字符串(String)
> 是我们的数据类型中的一种
> 是我们的基本数据类型(简单数据类型)中的一种
> 注意: 同时字符串也是一种包装数据类型 -> 包装数据类型 就是在存储的时候按照基本数据类型进行保存 当使用的时候瞬间转换成复杂数据类型进…
jmeter学习(7)beanshell
beanshell preprocessor
发送请求前执行
beanshell postprocessor
发送请求前执行 获取请求相关信息
String body sampler.getArguments().getArgument(0).getValue(); String url sampler.getPath();
获取响应报文 String responseprev.getResponseDataAsString();
获…
Android Studio Koala Feature Drop 稳定版现已推出
作者 / Android Studio 产品经理 Sandhya Mohan Android Studio Koala Feature Drop (2024.1.2) 现已推出!🐨 🔗 Android Studio https://developer.android.google.cn/studio 今年早些时候,我们宣布每个 Android Studio 动物版本…
quic-go实现屏幕广播程序
最近在折腾quic-go, 突然想起屏广适合用udp实现,而http3基于quic-go,后者又基于udp, 所以玩一下。
先贴出本机运行效果图:
功能(实现)说明:
1.服务器先启动作为共享屏幕方,等待客户端连接上来 2.客户端连接 3.客户…
集成Spring Cloud Alibaba AI大模型
一、申请api-key
官网地址:https://bailian.console.aliyun.com/#/home
二、代码实现
2.1 pom配置
<?xml version"1.0" encoding"UTF-8"?>
<project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http…
发送邮件和随机码的生成
类视图和方法视图区别: 不需要装饰器,只需要继承MethodView,需要使用什么方式就写对应的方法名称,它就能自动匹配 app.route("/delete/",methods["DELETE"])这些就不用写了 但是不写装饰器并不意味着不写路由了ÿ…
【AAOS】Android Automotive 9模拟器源码下载及编译
源码下载
repo init -u https://android.googlesource.com/platform/manifest -b android-9.0.0_r61
repo sync -c --no-tags --no-clone-bundle
源码编译
source build/envsetup.sh
lunch aosp_car_x86_64-userdebug
make -j8
运行效果
emulator Home界面 MAP All apps S…
dfs +剪枝sudoku———poj2676
目录 前言 lowbit函数 数独
suduku 问题描述 输入 输出
问题分析 子网格位置 优化搜索顺序剪枝1 优化搜索顺序剪枝2 可行性剪枝
代码 前言 lowbit函数 这是一个利用二进制位运算取出二进制数最后一位’1‘的函数 数独 数独大家肯定都玩过,…
【C语言复习】常见概念(零基础)
【C语言复习】常见概念 1、C语言是什么?2、C语言的历史和辉煌3、 编译器的选择VS20223.1编译和链接3.2编译器的对比3.3 VS2022 的优缺点 4、VS项⽬ 和 源⽂件、头⽂件介绍5、第一个C语言程序6、main函数(主函数)7、printf和库函数8、关键字介…
【高等代数笔记】线性空间(十九-二十四上半部分)
课程视频剪辑得太抽象了,一节课不能完整学完,拆的零零散散得。
3. 线性空间
3.19 满秩矩阵
【推论4】设 rank ( A ) r \text{rank}(\boldsymbol{A})r rank(A)r,则 A \boldsymbol{A} A的不为0的 r r r阶子式所在的列(行&#x…