本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/112333.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
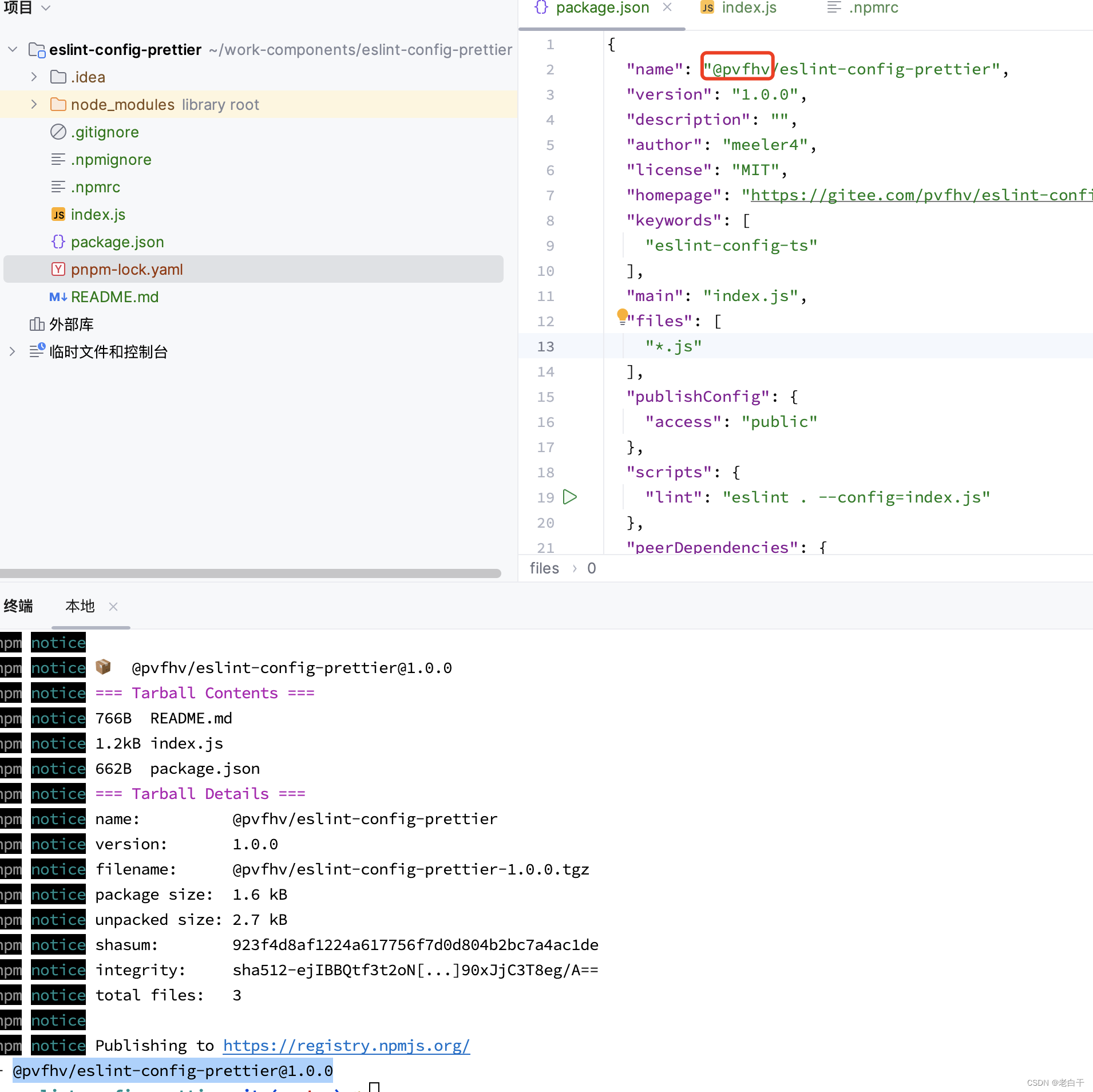
npm publish包报404,is not in the npm registry错误
1. 指定发布目标2. 登录npm,使用登录名发布包,包名命名原则“登录名/包名”,或 “包名” 3. 删除某一个版本npm unpublish pvfhv/eslint-config-prettier1.0.1 --force
删除后的版本不能重复使用,正式解释:
Unfortun…
Spring系列文章:Bean的获取⽅式
一、简介
Spring为Bean提供了多种实例化⽅式,通常包括4种⽅式。(也就是说在Spring中为Bean对象的创建准 备了多种⽅案,⽬的是:更加灵活)
第⼀种:通过构造⽅法实例化
第⼆种:通过简单⼯⼚模式…
SQL5 将查询后的列重新命名
描述
题目:现在你需要查看前2个用户明细设备ID数据,并将列名改为 user_infos_example,,请你从用户信息表取出相应结果。 示例:user_profile
iddevice_idgenderageuniversityprovince12138male21北京大学Beijing23214male复旦大学…
fastadmin的入门
fastadmin入门到完成项目
配置环境
1 运行环境 PHP > 7.2 且 < 7.4 (推荐PHP7.4版本) MySQL > 5.6 且 < 8.0 (需支持innodb引擎) Apache 或 Nginx 使用PHPstudy 运行该项目 写好apache伪静态规则
<IfModule mod_rewrite.c>
Options FollowSymlinks -Multi…
OpenCV(三十七):拟合直线、三角形和圆形
1.点集拟合的含义 点集拟合是一种通过拟合函数或曲线来近似描述给定离散数据点的技术,在点集拟合中,可以使用不同的函数或曲线拟合方法来拟合直线、三角形和圆形。
直线拟合:对于给定的二维数据点集合,可以使用最小二乘法来拟合一条直线。
…
Python 之 numpy.unique函数的介绍以及使用
文章目录 介绍语法:返回值:示例:补充[1] 介绍
np.unique 是 NumPy 库中的一个函数,用于从数组中获取唯一的值,并且可以返回这些唯一值的一些相关信息。以下是对 np.unique 函数的详细介绍:
语法ÿ…
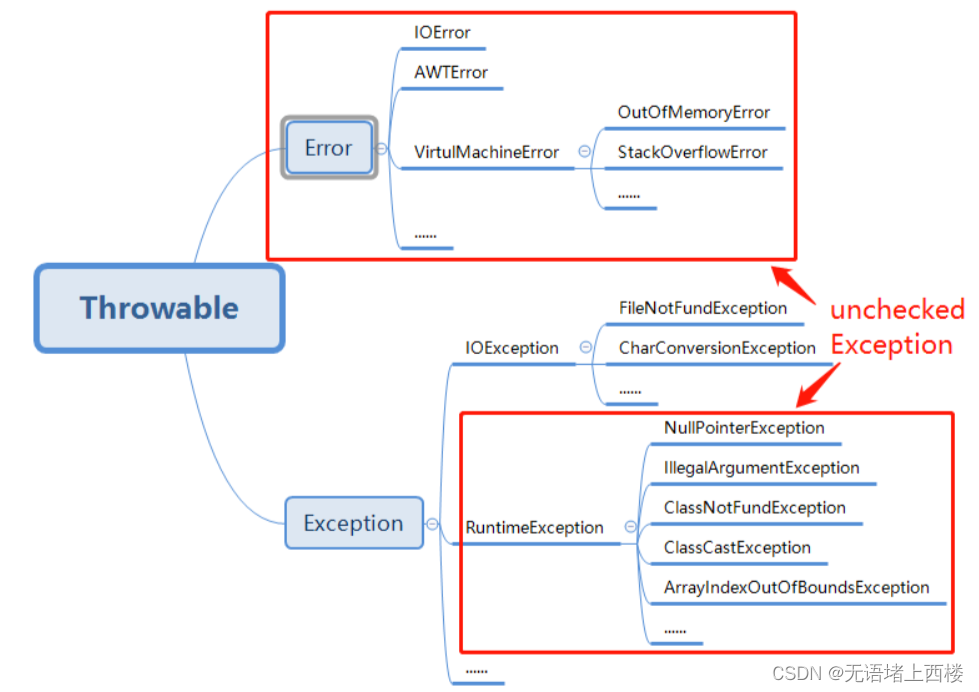
受检异常和非受检异常
异常 非受检异常和受检异常,都是继承自 Throwable 这个类中,分别是 Error 和 Exception, Error 是程序报错,系统收到无法处理的错误消息,它和程序本身无关。 Excetpion 是指程序运行时抛出需要处理的异常信息如果不主…
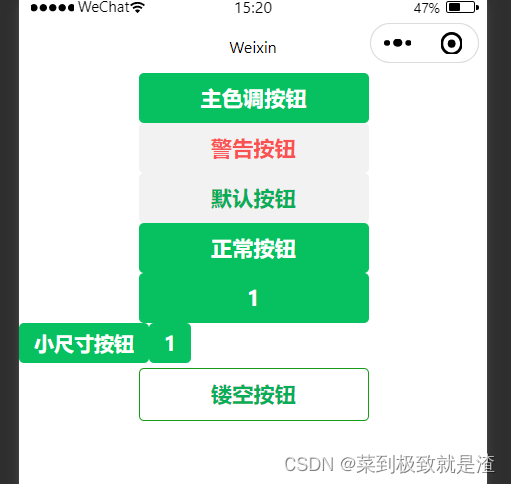
微信小程序开发---基本组件的使用
目录
一、scroll-view
(1)作用
(2)用法
二、swiper和swiper-item
(1)作用
(2)用法
三、text
(1)作用
(2)使用
四、rich-tex…
vs2019配置sfml外部库出现的问题
问题描述
在debug模式下程序正常运行,在release模式中报错
解决
C/C Windows环境下 boost 安装使用教程
Debug 通常称为调试版本,它包含调试信息,并且不作任何优化,便于程序员调试程序。 Release:Release通常称为发…
2023高教社杯数学建模A题思路分析 - 定日镜场的优化设计
# 1 赛题 A 题 定日镜场的优化设计
构建以新能源为主体的新型电力系统, 是我国实现“碳达峰”“碳中和”目标的一项重要 措施。塔式太阳能光热发电是一种低碳环保的新型清洁能源技术[1]。 定日镜是塔式太阳能光热发电站(以下简称塔式电站)收集太阳能的基本组件&…
Android USB电源管理
The USB peripheral detects the lack of 3 consecutive SOF packets as a suspend request from the USB host. 1 驱动shutdown顺序 系统关机或重启的过程中,会调用设备驱动的shutdown函数来完成设备的关闭操作,有需要的设备可以在驱动中定义该函数。其…
面试京东软件测试岗,收到offer后我却毫不犹豫拒绝了....
我大学学的是计算机专业,毕业的时候,对于找工作比较迷茫,也不知道当时怎么想的,一头就扎进了一家外包公司,一干就是2年。我想说的是,但凡有点机会,千万别去外包!
在深思熟虑过后&am…
Java从入门到精通-类和对象(一)
0. 类和对象 1. 面向对象概述 Java面向对象编程(Object-Oriented Programming,OOP)是一种强大的编程范式,它基于对象、类、封装、继承和多态等核心概念。这种编程范式使得代码更加模块化、可维护、可重用和可扩展。
1.1 对象和类…
大数据Flink(七十三):SQL的滚动窗口(TUMBLE)
文章目录
SQL的滚动窗口(TUMBLE) SQL的滚动窗口(TUMBLE)
滚动窗口定义:滚动窗口将每个元素指定给指定窗口大小的窗口。滚动窗口具有固定大小,且不重叠。例如,指定一个大小为 5 分钟的滚动窗口。在这种情况下,Flink 将每隔 5 分钟开启一个新的窗口,其中每一条数都会划…
胡焕庸线,我国东西地级市分布密度分界线
背景
黑河—腾冲线,又名胡焕庸线,是我国人口密度分布的东西近似分界线。今天把地级市坐标分布密度做成热力图,并与胡焕庸线一起展示时,惊奇的发现,胡焕庸线貌似也是我车东西地级市分布密度的分界线。
生成folium地图…
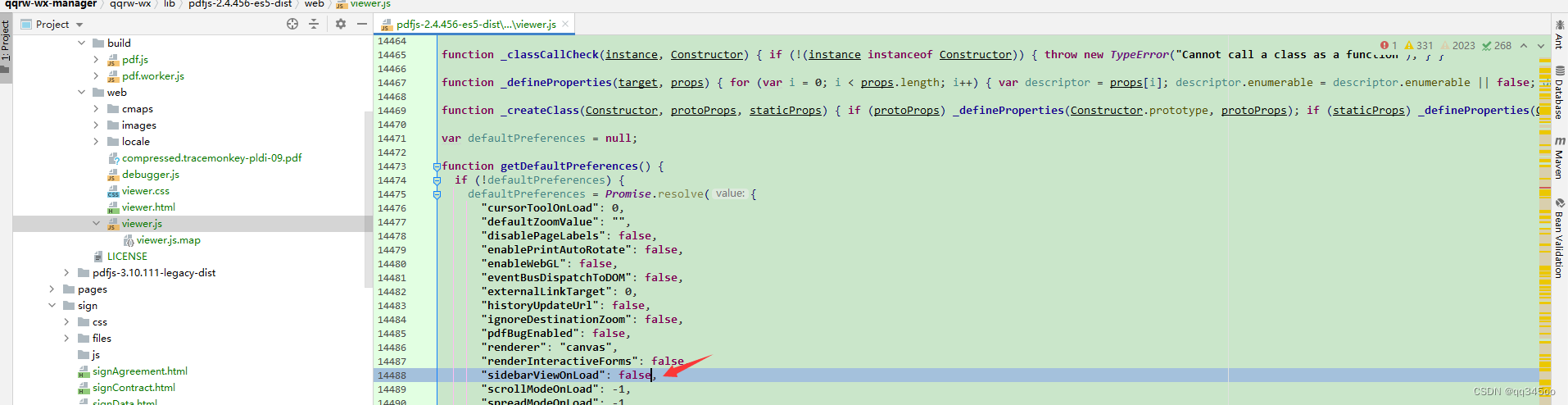
pdf.js 微信公众号不显示问题
问题1: 在浏览器中能够正常显示, 但是在微信浏览器中不行!解决: 这个是pdf.js 版本问题, 用2.4版本,微信打开就没问题了 问题2: 如何关闭侧边栏? 修改这个地方, 将 -1 改…
【C++11】{}初始化、std::initializer_list、decltype、STL新增容器
文章目录 1. C11简介2. 统一的列表初始化2.1 {}初始化2.2 std::initializer_list 3. 声明3.1 auto3.2 decltype 4. nullptr5. 范围for循环6. 智能指针7. C11STL中的一些变化8. 演示代码 1. C11简介 在2003年C标准委员会曾经提交了一份技术勘误表(简称TC1…
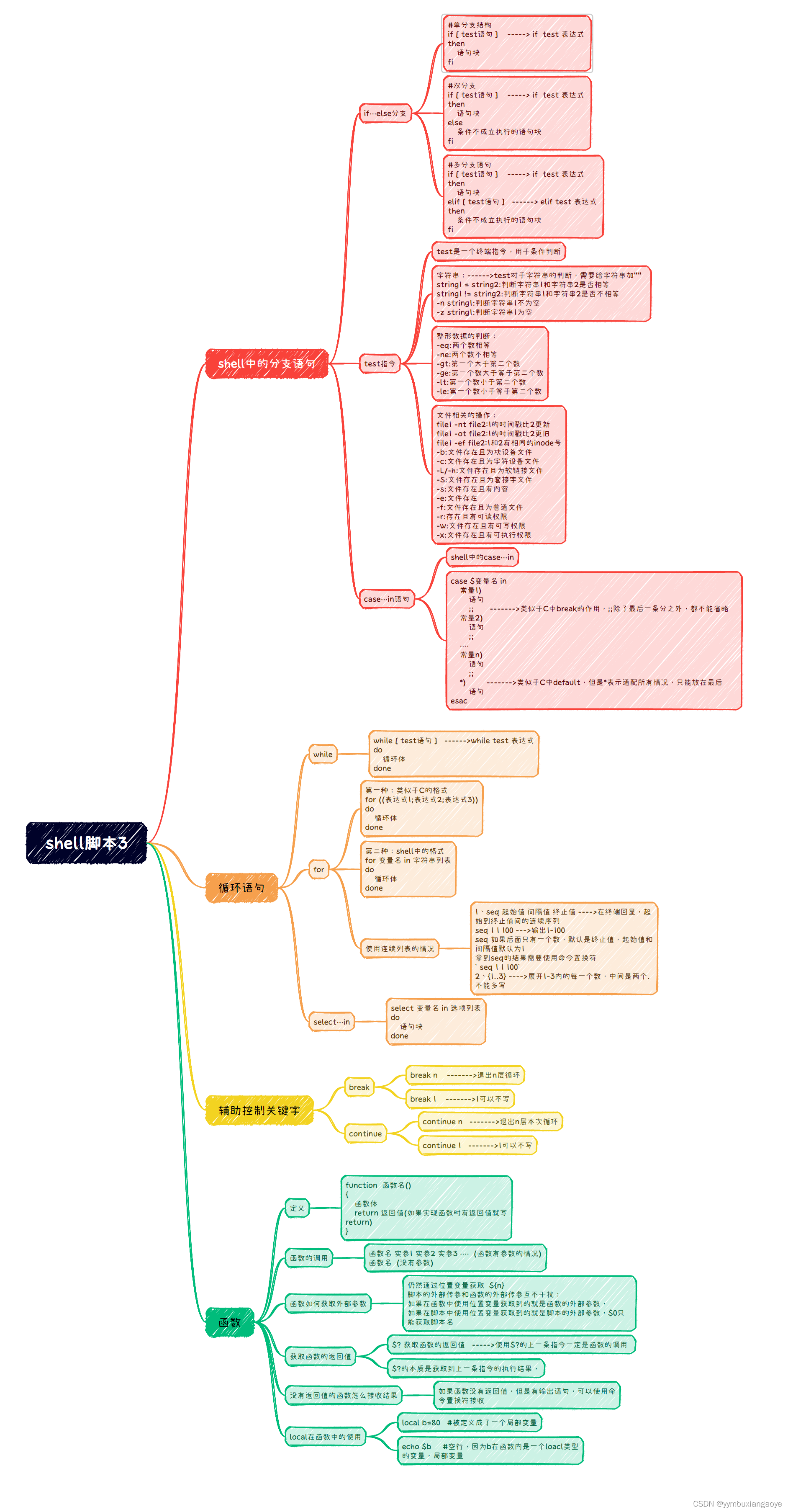
c高级day4(9.11)shell脚本(case ....in语句,循环语句,select ...in和case...In结合,辅助控制关键字,函数)
1.实现一个对数组就和的函数,数组通过实参传递给函数
2.写一个函数,输出当前用户的uid和gid,并使用变量接收结果
#!/bin/bash
read -a arr
sum0
function add()
{ …
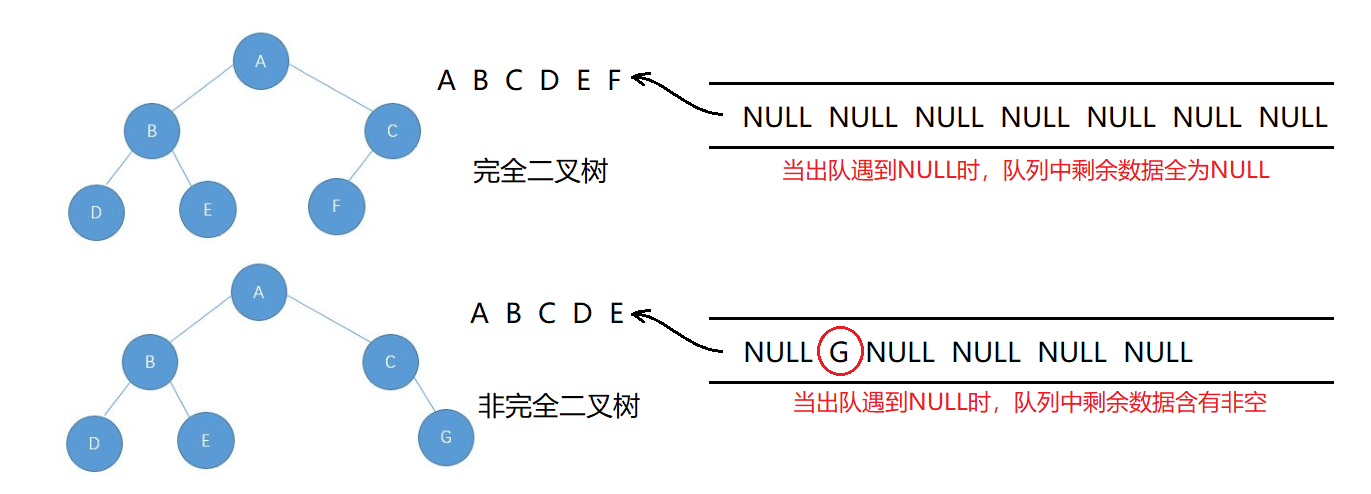
【数据结构】二叉树的链式存储结构
【数据结构】二叉树的链式存储结构
二叉树的存储结构
typedef int BTDataType;
// 二叉树的结构
typedef struct BinaryTreeNode {BTDataType data; // 树的值struct BinaryTreeNode *left; // 左孩子struct BinaryTreeNode *right;// 右孩子
} BinaryTreeNode;二…