本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.ldbm.cn/p/140558.html
如若内容造成侵权/违法违规/事实不符，请联系编程新知网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
Excel数据丢失怎么找回？详细恢复教程分享！
“我熬了好几个大夜才完成的一份Excel报表不知道为什么有些数据丢失了，现在处理起来很麻烦。有什么方法可以找回丢失的Excel数据吗？快帮帮我！” Excel作为一个强大的办公工具，我们在工作中经常都需要用到它。最令人崩溃的事就是有…
找不到msvcp140.dll解决方法的5个解决方法以及msvcp140.dll丢失原因分析
msvcp140.dll 是 Microsoft Visual C 2017 Redistributable 的一部分，许多应用程序和游戏都需要这个动态链接库（DLL）才能正常运行。如果您的系统中找不到 msvcp140.dll，您可能会遇到无法打开某些应用程序或游戏的困境。小编将讨论…
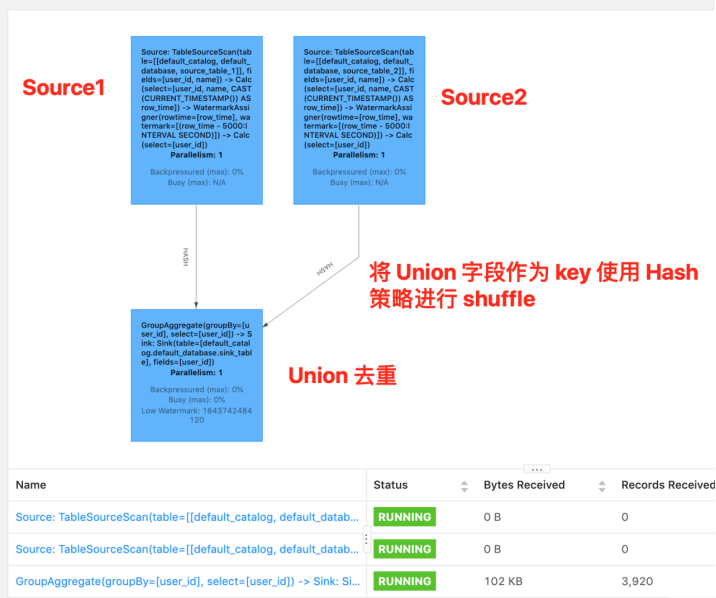
Windows权限维持
Meterpreter权限维持
Metasploit 框架提供了一个后渗透模块，可实现自动化地利用沾滞键的权限维持技术。 该模块将用 CMD 替换辅助功能的二进制文件（ sethc, osk, disp, utilman ）
use post/windows/manage/sticky_keys
设置session 提示&a…
计算机网络笔记 第二章 物理层
2.1 物理层概述
物理层要实现的功能 物理层接口特性
机械特性
形状和尺寸引脚数目和排列固定和锁定装置 电气特性
信号电压的范围阻抗匹配的情况传输速率距离限制 功能特性
-规定接口电缆的各条信号线的作用 过程特性
规定在信号线上传输比特流的一组操作过程࿰…
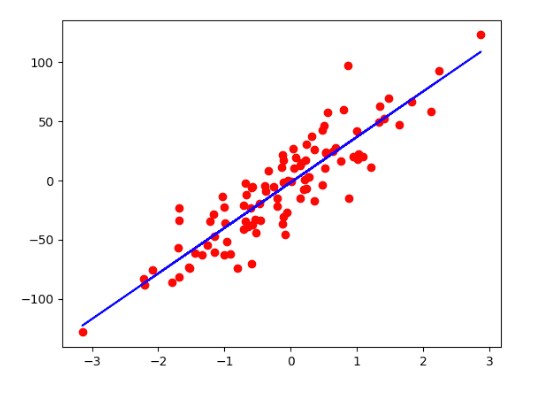
【人工智能导论】线性回归模型
一、线性回归模型概述
线性回归是利用函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。简单来说，就是试图找到自变量与因变量之间的关系。 二、线性回归案例：房价预测
1、案例分析 问题：现在要预测140平方的房屋的价格&…
gitlab配置webhook限制提交注释
一、打开gitlab相关配置项
vim /etc/gitlab/gitlab.rb
gitlab_shell[custom_hooks_dir] "/etc/gitlab/custom_hooks" 二、创建相关文件夹
mkdir -p /etc/gitlab/custom_hooks
mkdir -p /etc/gitlab/custom_hooks/post-receive.d
mkdir -p /etc/gitlab/custom_h…
【vue3】Suspense组件和动态引入defineAsyncComponent的搭配使用
假期第五篇，对于基础的知识点，我感觉自己还是很薄弱的。 趁着假期，再去复习一遍
在app中定义子组件child
//静态引入，网速慢的时候，父子组件也是同时渲染出来
<template><div><h3>APP父组件</…
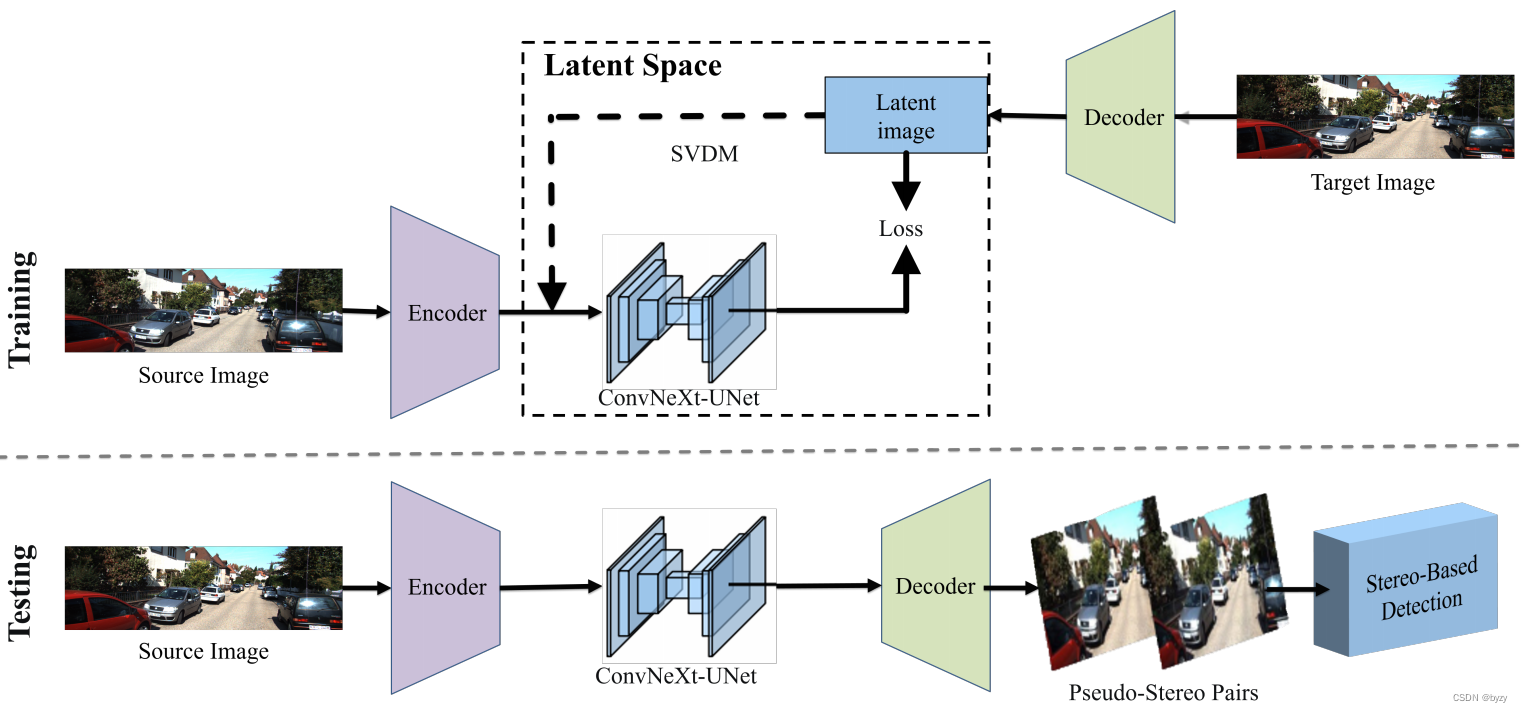
【论文笔记】SVDM: Single-View Diffusion Model for Pseudo-Stereo 3D Object Detection
原文链接：https://arxiv.org/abs/2307.02270
1. 引言 目前的从单目相机生成伪传感器表达的方法依赖预训练的深度估计网络。这些方法需要深度标签来训练深度估计网络，且伪立体方法通过图像正向变形合成立体图像，会导致遮挡区域的像素伪影、扭…
机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
机器人中的数值优化|【五】BFGS算法的非凸/非光滑处理
往期内容回顾
机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法，可行牛顿法的python实现，以Rosenbrock function为例 机器人中的数值优化|【三】无约束优化࿰…
线性代数(七) 矩阵分析
前言
从性线变换我们得出，矩阵和函数是密不可分的。如何用函数的思维来分析矩阵。
矩阵的序列 通过这个定义我们就定义了矩阵序列的收敛性。 研究矩阵序列收敛性的常用方法，是用《常见向量范数和矩阵范数》来研究矩阵序列的极限。 长度是范数的一个特…
bypass disable_function 学习
LD_PRELOAD
我是在做了 buu的 REC ME 来做这个系列
所以 LD_PRELOAD 已经有了解了
我们来做这个题目
CTFHub Bypass disable_function —— LD_PRELOAD本环境来源于AntSword-Labs
<!DOCTYPE html>
<html>
<head><title>CTFHub Bypass disable_func…
Flutter笔记 - 用于描述Align的Alignment、AlignmentDirectional、AlignmentTween类
Flutter笔记 用于描述Align的Alignment、AlignmentDirectional、AlignmentTween类 作者：李俊才 （jcLee95）：https://blog.csdn.net/qq_28550263 邮箱 ：291148484163.com 本文地址：https://blog.csdn.net/qq_…
基于Java的服装销售平台设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序（小蔡coding）有保障的售后福利 代码参考源码获取 前言 💗博主介绍：✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…
Armv8/Armv9 Cache知识大纲分享--思维导图
关键词：cache学习、mmu学习、cache资料、mmu资料、arm资料、armv8资料、armv9资料、 trustzone视频、tee视频、ATF视频、secureboot视频、安全启动视频、selinux视频，cache视频、mmu视频，armv8视频、armv9视频、FF-A视频、密码学视频、RME/CC…
![2023年中国智能电视柜产量、需求量、市场规模及行业价格走势[图]](https://img-blog.csdnimg.cn/img_convert/f189ab4f3166845d1771bce82cd76bdf.png)
2023年中国智能电视柜产量、需求量、市场规模及行业价格走势[图]
电视柜是随着电视机的发展和普及而演变出的家具种类，其主要作用是承载电视机，又称视听柜，随着生活水平的提高，与电视机相配套的电器设备也成为电视柜的收纳对象。 随着智能家具的发展，智能电视机柜的造型和风格都是有了…
Jmeter如何做压力测试
1.哪些业务需要做压力测试？
比较常用的业务场景或功能模块
单业务场景或多业务场景
项目要求做的业务场景
2.压力测试的并发数是多少？
有预期的数值？100 200 300一次性达到还是逐次增加？参照上次性能测试的结果
3.关注哪些参…
计算机网络学习易错点
目录
概述
1.internet和Internet的区别
2.面向连接和无连接
3.不同的T
4.传输速率和传播速率
5.传播时延和传输时延（发送时延）
6.语法，语义和同步
一.物理层
1.传输媒体与物理层
2.同步通信和异步通信
3.位同步（比特同…
Jmeter状态码及请求
Jmeter与LR的区别? 1.都是压测工具，可以用来做性能测试，但是Jmeter比较轻量级。jmeter 是用java语言写的，需要java环境，LR不需要，除非用iavavuser协议 (不用掌握) 2.Jmeter更偏向于功能和技术，LR偏向于业务…
AnyDesk多ID集中控制台V2.0
网盘下载 AnyDesk多ID集中控制台V2.0 软件介绍： 首先大家要知道AnyDesk软件是干嘛的？国外的远程协助工具，和TeamViewer同一个软件，TeamViewer确定需要登录，使用限制5分钟等等缺点，所以自己就用易语言开发An…