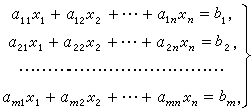本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/147234.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
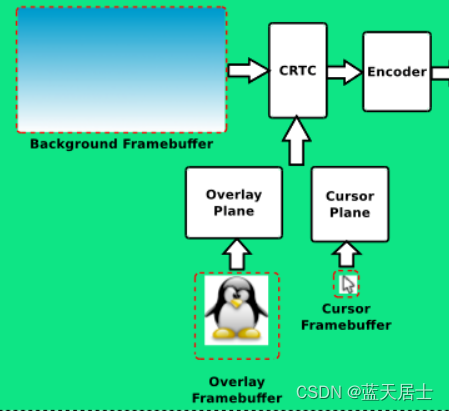
DRM全解析 —— CRTC详解(1)
本文参考以下博文:
Linux内核4.14版本——drm框架分析(4)——crtc分析
特此致谢! 1. 简介
CRTC实际上可以拆分为CRTC。CRT的中文意思是阴极摄像管,就是当初老电视上普遍使用的显像管(老电视之所以都很厚,就是因为它…
计算机网络 第二章物理层
计算机网络第二章知识点速刷 其中重要的是信源和信宿,以及调制解调器在通信模型当中起到的作用。 单工、半双工和全双工。 调制和解调。编码和解码。 数据通信基础 - 比特率(bit/s)与 波特率(Baud)换算
我在假期用ttkefu成交了6单生意
在这个假期里,我有幸体验了TTKEFU客服软件,并成功地利用它成交了6单。这次经历让我深刻体会到了TTKEFU客服软件的强大功能和实用性,也让我对自己的沟通能力有了更高的要求。在此,我想分享一下我的心得体会,希望能对大家…
flac文件怎么转换成mp3?非常使用的3个方法
flac文件怎么转换成mp3?FLAC(Free Lossless Audio Codec)是一种自由开源的无损音频编码格式,它被广泛用于音频的压缩和存储。与其他有损音频编码格式(如MP3)不同,FLAC能够以无损的方式压缩音频数…
电脑PC端有哪些好用的记笔记工具
在日常学习中,想要学好每一门学科,必定离不开使用笔记软件记录,如何高效记录学习笔记呢?电脑PC端记录学习笔记用哪一款工具比较好呢?今天给大家推荐一款功能比较齐全的多平台记笔记工具——敬业签。
学生们通常不仅在…
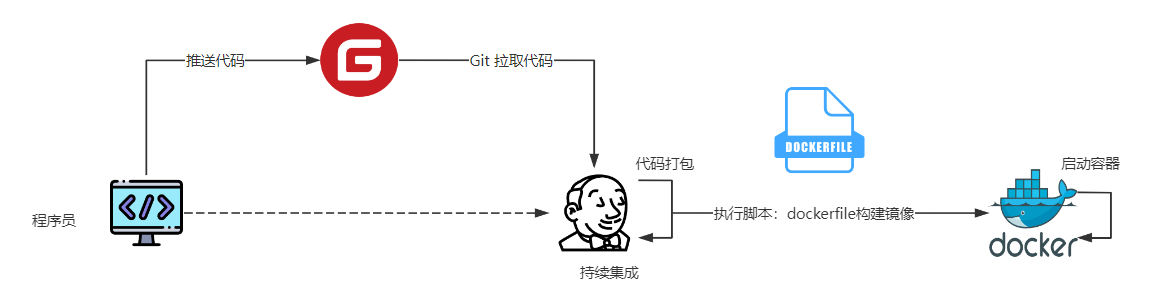
五.docker+jenkins自动部署项目
一.敏捷开发相关概念
1.微服务的痛点
再来看一下我们的微服务架构 , 每个组件都需要服务器去部署,加起来可能需要几十个甚至上百个服务器。这样的微服务项目在部署上会遇到什么问题?
需要很多很多的服务器,服务器的采购安装&am…
微信如何防止被限制?一文了解原因和处理方法
微信引流频繁被限制加好友,是许多人在营销过程中遇到的一大难题。为了解决这一问题,我们需要先了解微信官方对好友添加的限制和政策。只有明确了这些规定,才能更有效地进行微信引流,提高营销效果。 为什么被限制? 为了…
哨兵(Sentinel-1、2)数据下载
哨兵(Sentinel-1、2)数据下载
一、登陆欧空局网站 二、检索 先下载2号为光学数据 分为S2A和S2B,产品种类有1C和2A,区别就是2A是做好大气校正的影像,当然数量也会少一些,云量检索条件中记得要按格式&#x…
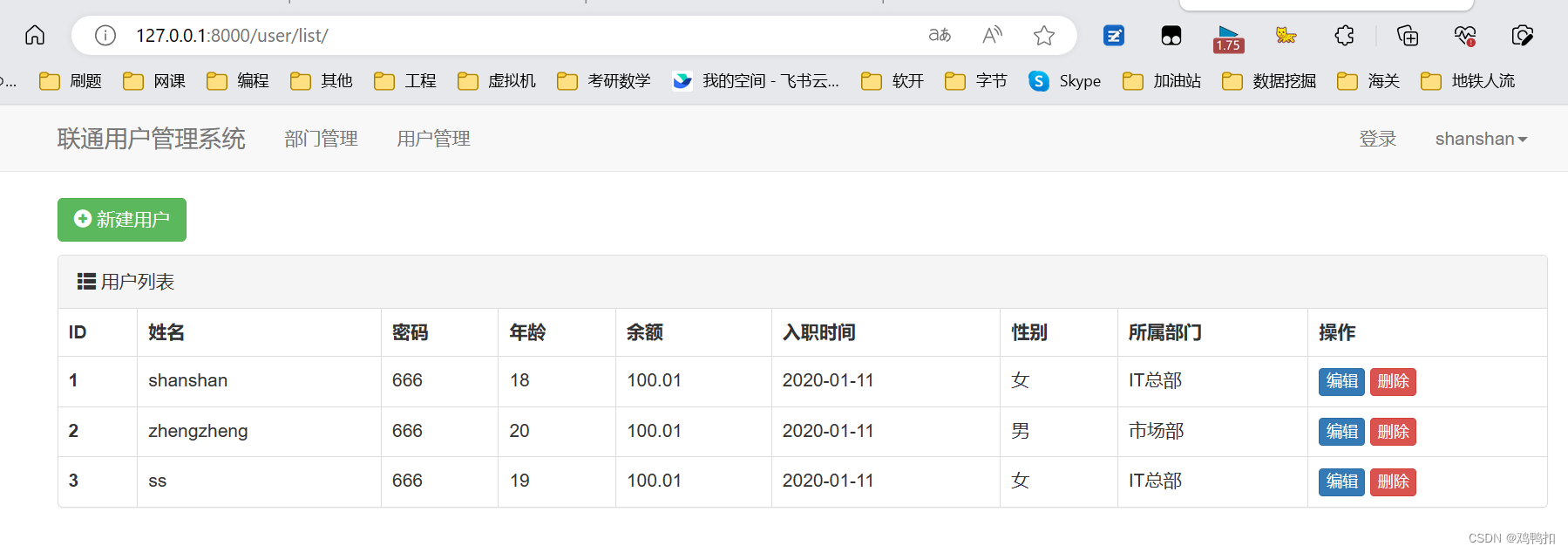
十二、Django之模板的继承+用户列表
模板的继承
新建layout.html:
{% load static %}
<!DOCTYPE html>
<html lang"en">
<head><meta charset"UTF-8"><title>Title</title><link rel"stylesheet" href"{% static plugins…
外卖小程序源码vs定制开发:何时选择哪种方式?
在数字餐饮行业的蓬勃发展中,外卖应用程序已经成为餐厅和创业者的必备工具。然而,当涉及到开发外卖应用程序时,您会面临一个重要的决策:是使用外卖小程序源码还是进行定制开发?这两种方法各有优势和劣势,取…
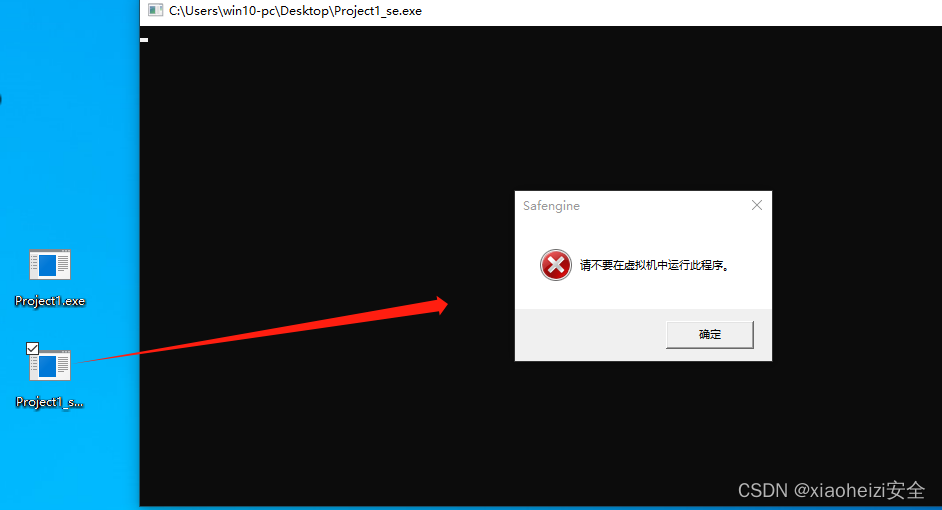
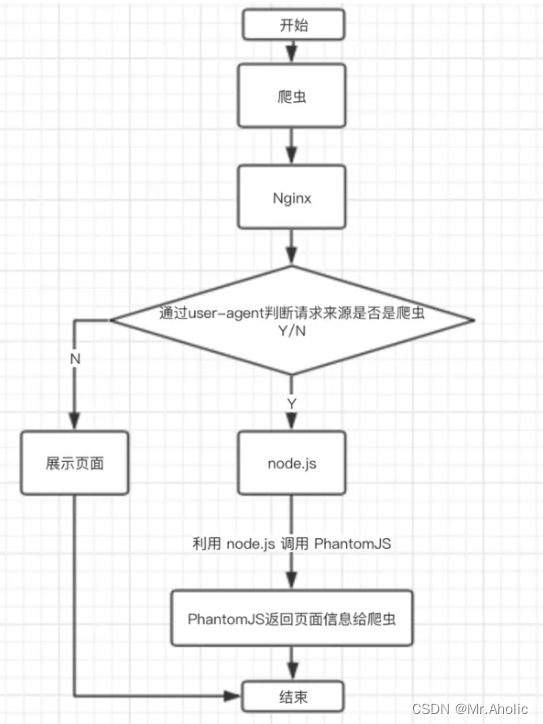
免杀对抗-反沙盒+反调试
反VT-沙盒检测-Go&Python 介绍: 近年来,各类恶意软件层出不穷,反病毒软件也更新了各种检测方案以提高检率。 其中比较有效的方案是动态沙箱检测技术,即通过在沙箱中运行程序并观察程序行为来判断程序是否为恶意程序。简单来说…
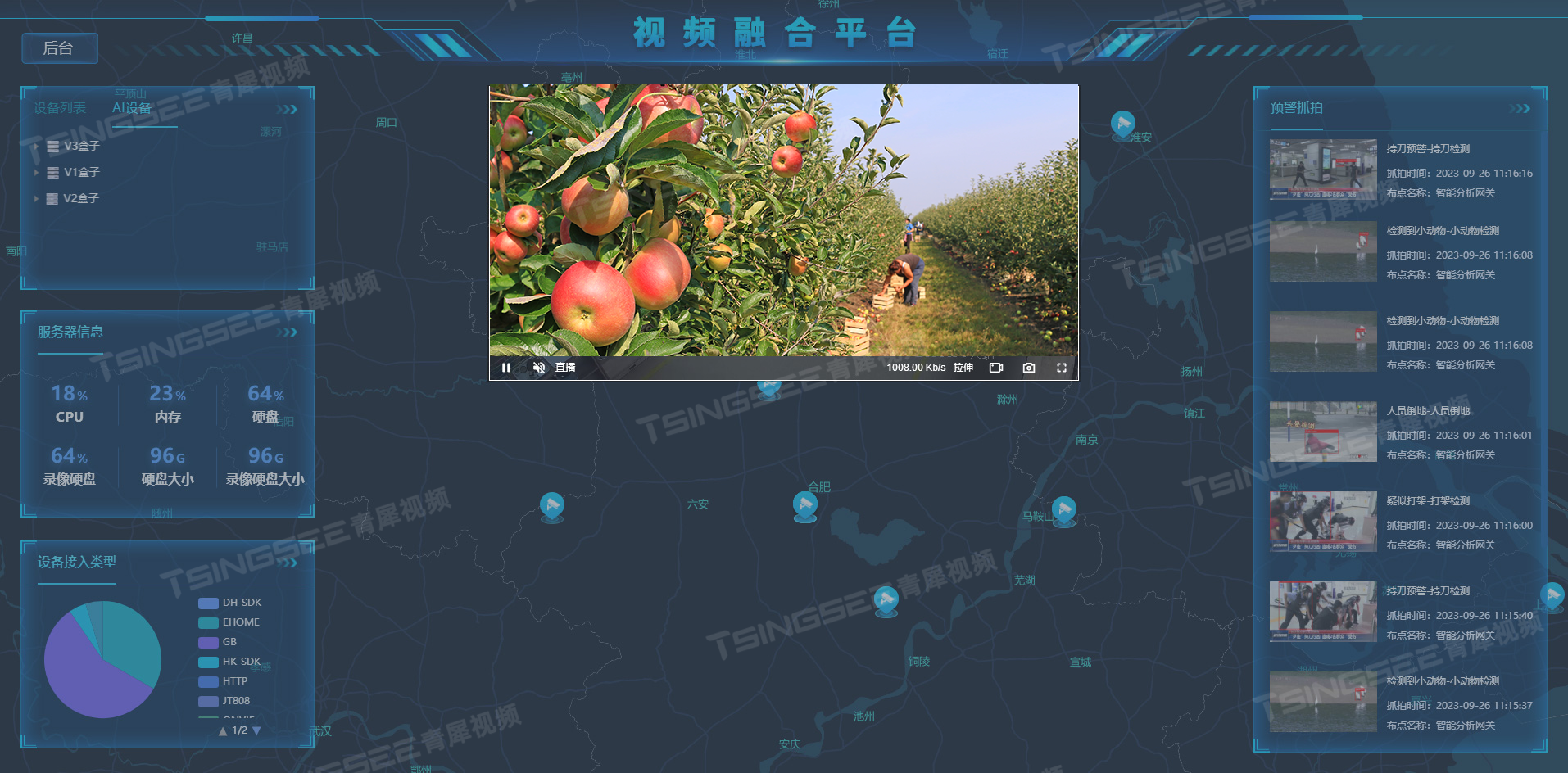
水果种植与果园监管“智慧化”,AI技术打造智慧果园视频综合解决方案
一、方案背景
我国是水果生产大国,果园种植面积大、产量高。由于果园的位置大都相对偏远、面积较大,值守的工作人员无法顾及到园区每个角落,因此人为偷盗、野生生物偷吃等事件时有发生,并且受极端天气如狂风、雷暴、骤雨等影响&a…
为什么越来越多的人转行网络安全?
为什么越来越多的人转行网络安全?
目前,我国互联网已经从前期的爆发增长进入稳定发展阶段,同时每年大量计算机相关专业的毕业生进入就业赛道,导致IT行业逐渐趋于饱和状态,甚至出现裁员现象,去年很多大厂都…
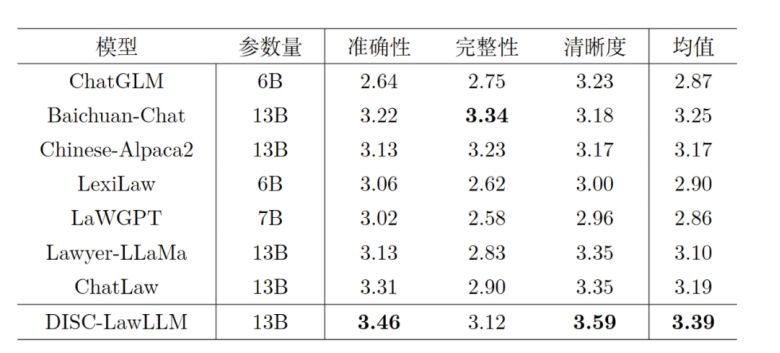
AI颠覆法律行业,律师要失业了?
如果要说一个 AI 真正起飞,并且对行业从业者带来的更多是正面影响的垂直行业,小编觉得在目前阶段,法律可以算一个。这个行业有几个特点:对人的依赖很大,专业性很强,大量繁复的文字工作。因此,在…
【Vue面试题二】、说说你对SPA (单页应用) 的理解?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:你对SPA单页面的理解&am…
883. 高斯消元解线性方程组
883. 高斯消元解线性方程组 - AcWing题库 输入一个包含 n 个方程 n 个未知数的线性方程组。
方程组中的系数为实数。
求解这个方程组。
下图为一个包含 m 个方程 n 个未知数的线性方程组示例: 输入格式
第一行包含整数 n。
接下来 n 行,每行包含 n1…
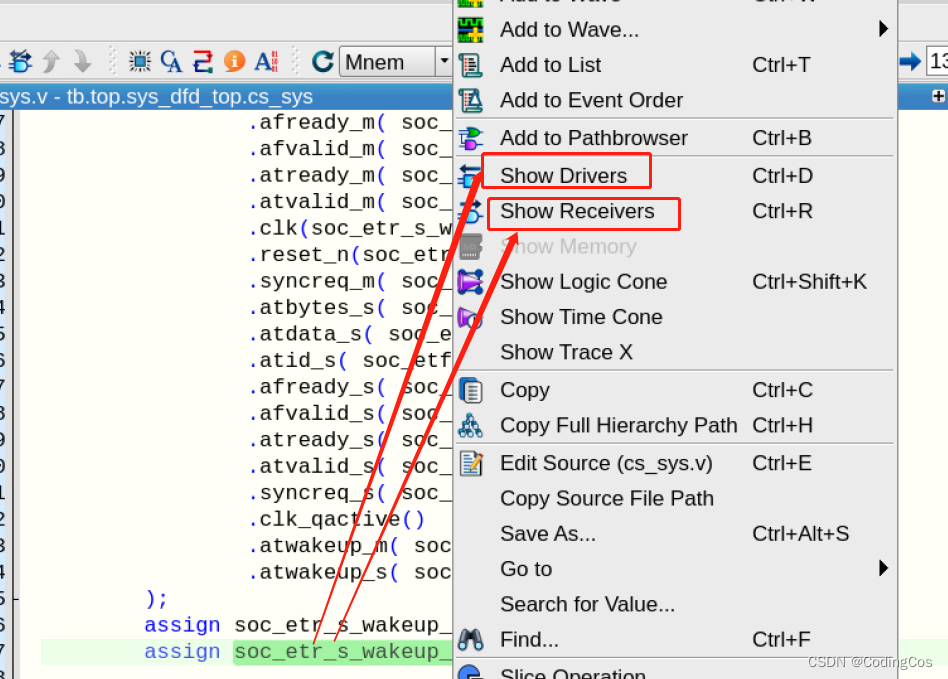
【芯片设计- RTL 数字逻辑设计入门 4 - 第一个 RTL Bug 分析之路 】
文章目录 1.1 Veloce 验证1.1.1 问题背景1.1.2 问题分析1.1.3 调试小技巧 1.1 Veloce 验证
本文是基于veloce验证平台进行的,关于veloce的介绍如下:
传统的验证技术中,主要采用两种手段。
一种是基于EDA工具(Simulator)的仿真验证。这种验证方式是基于…
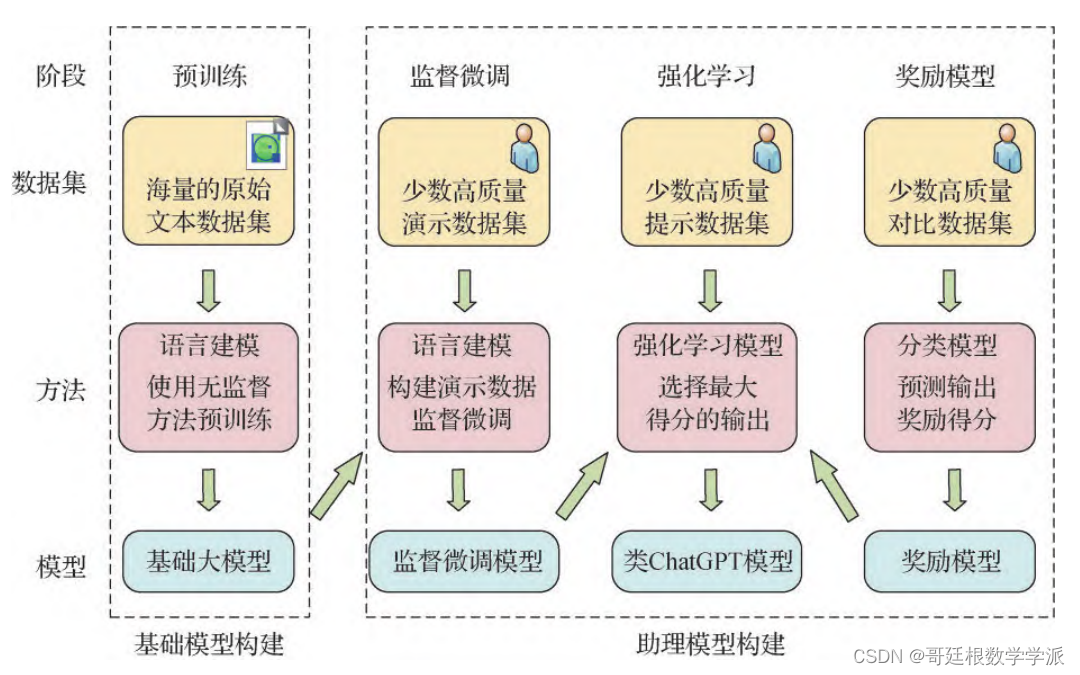
类 ChatGPT 模型存在的局限性
尽管类ChatGPT模型经过数月的迭代和完善,已经初步融入了部分领域以及人们的日常生活,但目前市面上的产品和相关技术仍然存在一些问题,以下列出一些局限性进行详细说明与成因分析:
1)互联网上高质量、大规模、经过清洗…
基于vue框架的uniapp小程序开发发现了新大陆
项目场景:
在基于vue框架的uniapp小程序开发中,在页面跳转时,当前页路径带参数,在跳转页中接受数据除了用官方推荐的保留当前页面,跳转到应用内的某个页面,使用onLoad(option)接受数据,但是我发…