本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/261888.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
for循环定义域问题
记录一个偶然发现的问题,代码如下
int main(int argc, char *argv[], char *envp[]){for(int i 1; i < 10; i);printf("%d",i); return 0;
}
可以看到for循环后加了一个分号,按理说应该报变量i未定义的错误,但此时在编译器中…
centos7 yum安装nginx
1.安装源
yum install epel-release
2.安装 (-y 的意思是自动yes)
yum install nginx -y
3.查找安装到哪里了
whereis nginx
一般都是在 /etc/nginx下面 4.常用命令 检查配置文件是否正确 nginx -t 启动 systemctl start nginx 查看状态 systemctl status nginx
设置开…
一起学docker系列之十五深入了解 Docker Network:构建容器间通信的桥梁
目录 1 前言2 什么是 Docker Network3 Docker Network 的不同模式3.1 桥接模式(Bridge)3.2 Host 模式3.3 无网络模式(None)3.4 容器模式(Container) 4 Docker Network 命令及用法4.1 docker network ls4.2 …
JavaScript 数据结构
JavaScript 数据结构
目录
JavaScript 数据结构
一、标识符
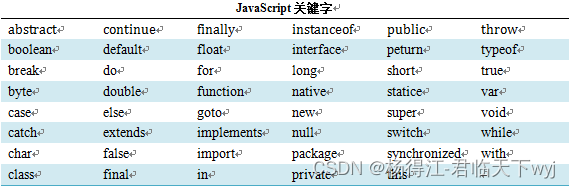
二、关键字
三、常量
四、变量 每一种计算机编程语言都有自己的数据结构,JavaScript脚本语言的数据结构包括:标识符、常量、变量、保留字等。 一、标识符
标识符,说白了&…
15、 深度学习之正向传播和反向传播
上一节介绍了训练和推理的概念,这一节接着训练和推理的概念讲一下,神经网络的正向传播和反向传播。
其实单看正向传播和反向传播这两个概念,很好理解。
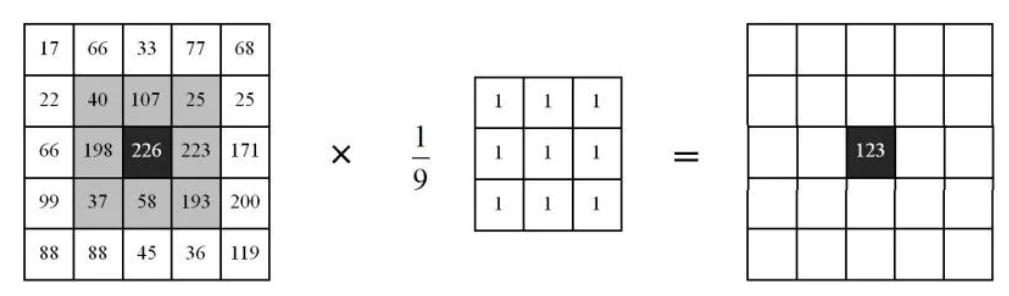
正向传播(Forward Propagation)是指从输入层到输出层的数据流动过程,而反向传播(Backpropagation)是指数据从输出…
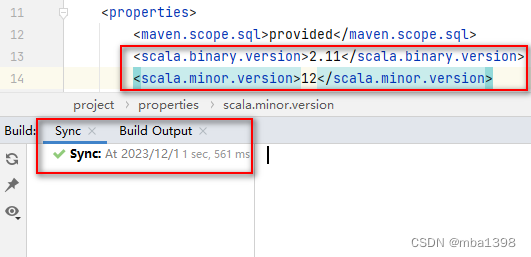
【已解决】Cannot find project Scala library 2.11.8 for module XXX
问题描述
在 flink 示例程序调试过程中,reload project 报错 Cannot find project Scala library 2.11.8 for module HbasePrint 报错如下图所示:
问题解决
经过搜索,初步判定是 pom 文件中 Scala 版本配置和项目中实际使用的版本不一致导…
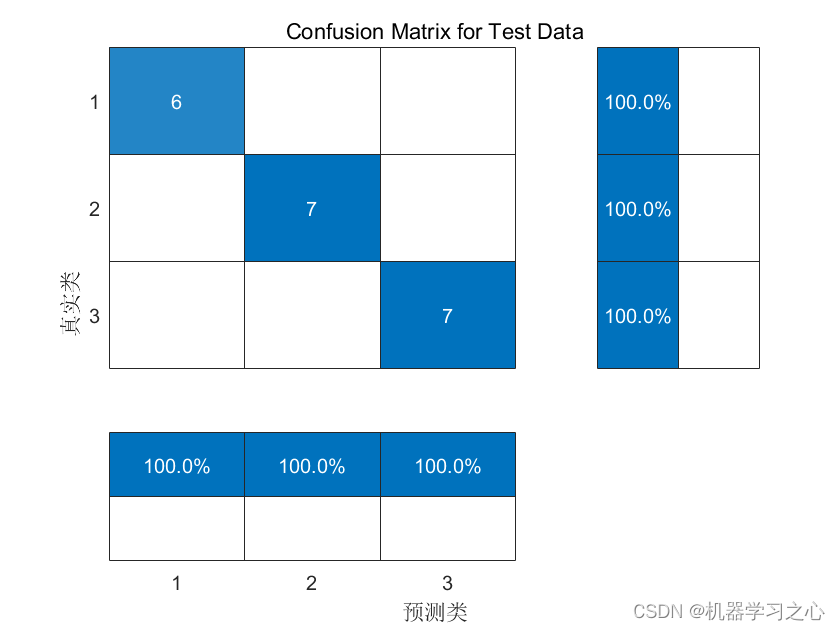
分类预测 | Matlab实现NGO-KELM北方苍鹰算法优化核极限学习机分类预测
分类预测 | Matlab实现NGO-KELM北方苍鹰算法优化核极限学习机分类预测 目录 分类预测 | Matlab实现NGO-KELM北方苍鹰算法优化核极限学习机分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现NGO-KELM北方苍鹰算法优化核极限学习机分类预测(完…
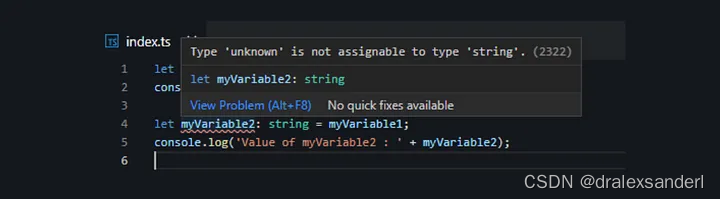
停止在 TypeScript 中使用 any 类型
停止在 TypeScript 中使用 any 类型
TypeScript 是 Web 开发人员中最常用的编程语言之一。它具有出色的语言功能,允许我们轻松设计可扩展的应用程序。因此,开发人员倾向于在项目中选择 TypeScript 而不是 JavaScript。
然而,在使用 TypeScr…
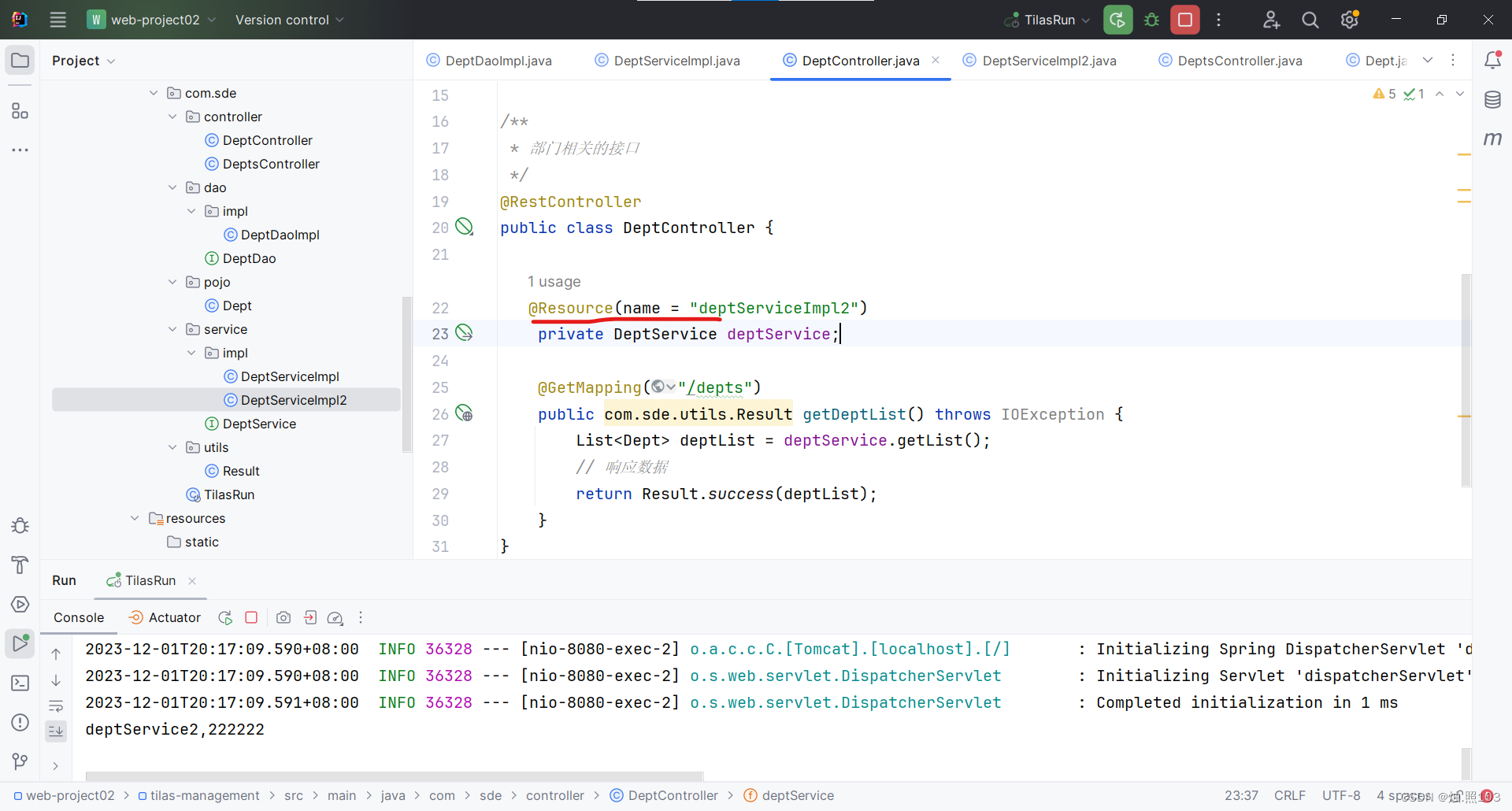
java开发实战 基于Resuful风格开发接口, IocDi和nginx,以及三层架构思想,分层解耦,并使用Apifox对接口数据进行测试。
开发规范: 前后端分离: 根据需求文档开发 Resultful风格: REST(REpresentational State Transfer),表述性状态转换,它是一种软件架构风格。 POST(insert) 负责新增的操作 http://localhost:8080…
【高效开发工具系列】驼峰下划线互转
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…
数学建模-基于LightGBM和BP神经网络的互联网招聘需求分析与预测
基于LightGBM和BP神经网络的互联网招聘需求分析与预测
整体求解过程概述(摘要) 就业是民生之本,是发展之基,也是安国之策。2020 年新冠肺炎疫情的爆发,稳就业成为应对疫情、稳定社会的重要保障之一。随着数据新动能的发展,互联网…
2023年多元统计分析期末试题
一、简答题
1、试述距离判别法、Fisher判别法和贝叶斯判别法的异同。
二、
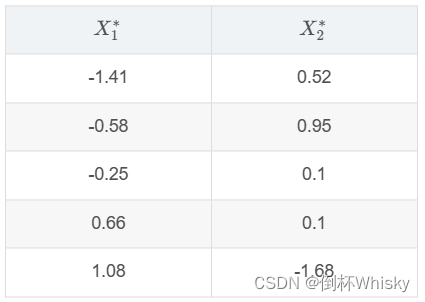
2、设 X {X} X~ N 2 {N_2} N2(μ,Σ),其中 X {X} X ~ ( X 1 {X_1} X1, X 2 {X_2} X2, X 3 {X_3} X3),μ ( μ 1 {μ_1} μ1, μ 2 {μ_2} …
【linux】日志有哪些
Linux系统日志主要有以下几种类型: 内核及系统日志:这种日志数据由系统服务rsyslog统一管理,根据其主配置文件/etc/rsyslog.conf中设置决定内核消息及各种系统程序消息记录到什么位置。/var/log/message:该日志文件存放了内核消息…
C语言每日一题(43)旋转链表
力扣 61 旋转链表
题目描述
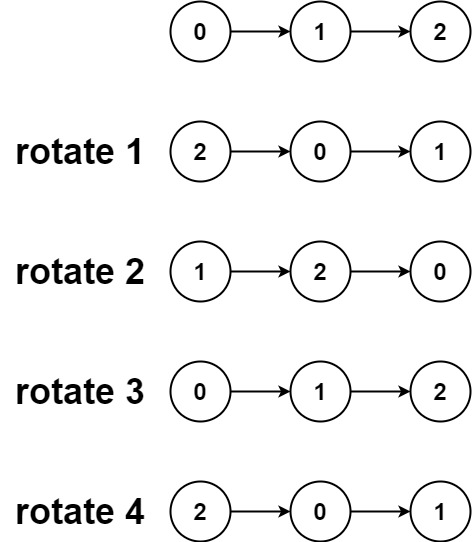
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。 示例 1: 输入:head [1,2,3,4,5], k 2
输出:[4,5,1,2,3]示例 2: 输入:head [0,1,2], …
UiPath:人工智能和重新加速增长是 2024 年的好兆头
UiPath(NYSE:PATH)重新加速增长,同时在销售和营销方面变得最高效,使其成为进入 2024 年的有吸引力的成长型股票。
UiPath 最初被归类为机器人流程自动化 (RPA) 公司,现在认为自己是一家人工智能驱动的自动…
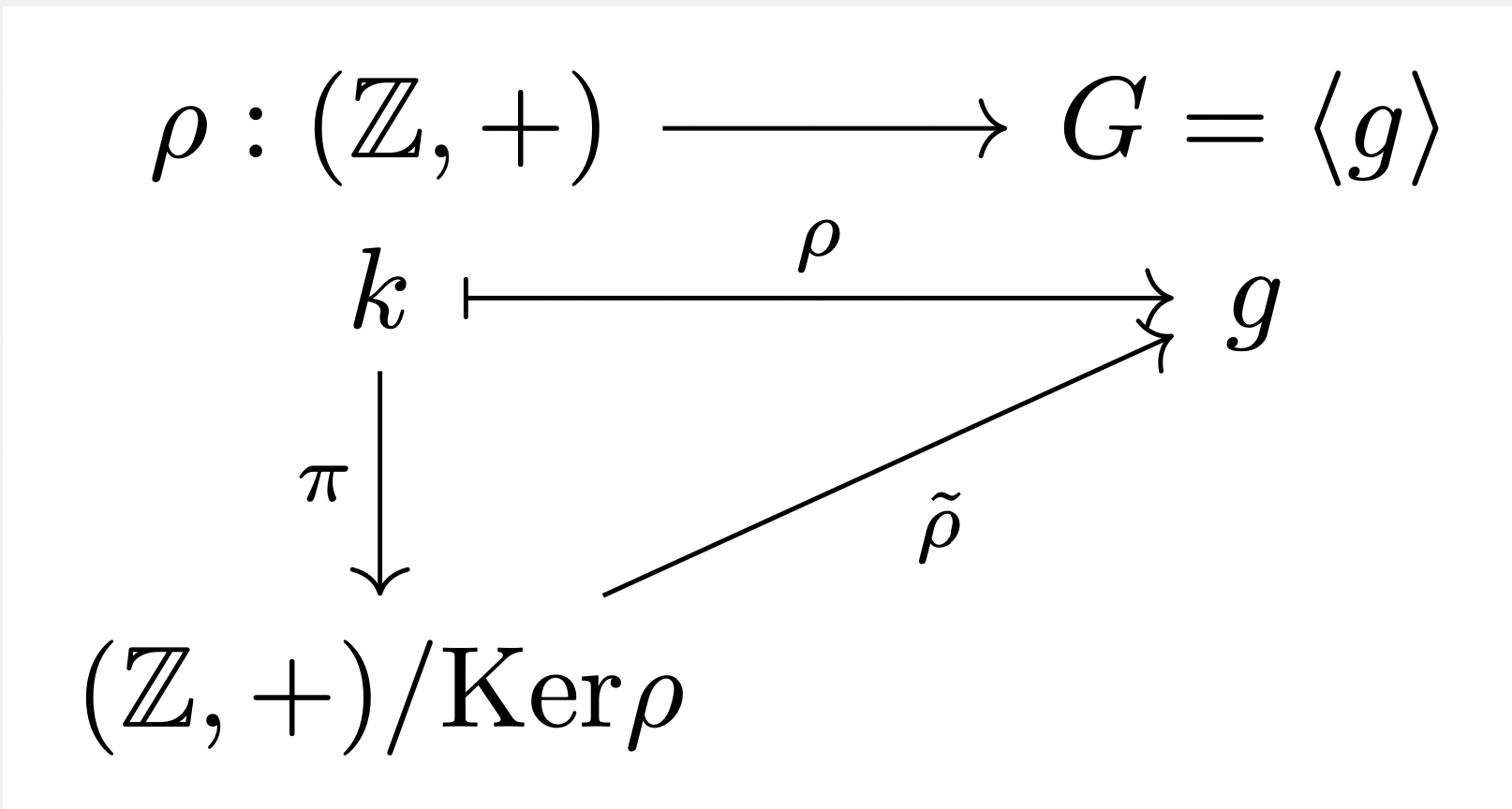
代数学笔记6: 群同态基本定理,循环群结构定理
群同态 ρ : G 1 ( , ⋅ ) → G 2 ( , ∘ ) g ↦ ρ ( g ) \rho:G_1(\ ,\cdot)\to G_2(\ ,\circ)\\ \qquad\ \ g\mapsto \rho(g) ρ:G1( ,⋅)→G2( ,∘) g↦ρ(g) ∀ g 1 , g 2 ∈ G \forall g_1,g_2\in G ∀g1,g2∈G, 有 ρ ( g 1 ⋅ g 2 ) ρ ( g 1 ) ∘ ρ ( g 2 …