本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/308973.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
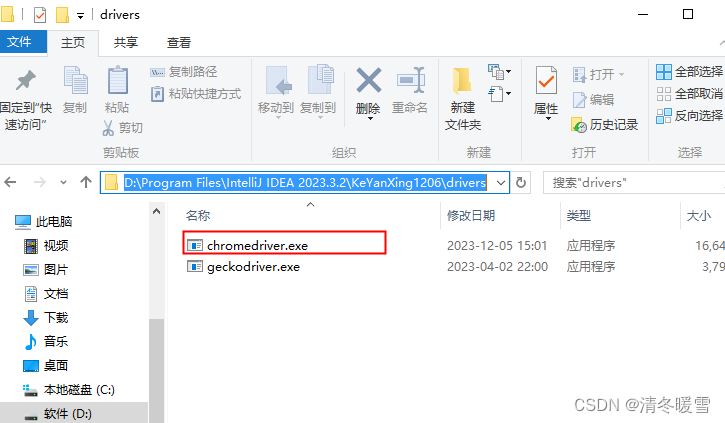
谷歌浏览器安装不在默认安装位置Selenium无法打开解决方法
Selenium之cannot find Chrome binary错误-CSDN博客
上面是我找的解决方案的链接
通过option.setBinary()的方法来指定谷歌浏览器的实际运行文件路径;
下面是结合我这边具体情况下写的代码
option.setBinary()中的路径是谷歌浏览器运行文件的路径;Sy…
2024年1月1日孙溟㠭篆刻艺术展开幕式于北京大学北大书店成功举办
“印记青春——会说话的石头” 主题文化展盛大开幕 2024年1月1日正值新年伊始,由北京大学出版社、北大书店、不黑文化艺术学社、中国诗书画研究会三才书画院联合举办的“印记 青春——会说话的石头”主题篆刻艺术展,在北京大学新太阳学生中心拉开帷幕。 …
非常好用的个人工作学习记事本Obsidian
现在记事本有两大流派:Obsidian 和Notion,同时据说logseq也很不错
由于在FreeBSD下后两种都没有相关ports,所以优先尝试使用Obsidian
Obsidian简介
Obsidian是基于Markdown文件的本地知识管理软件,并且开发者承诺Obsidian对于个…
【Docker】快速入门之Docker的安装及使用
一、引言 1、什么是Docker Docker是一个开源的应用容器引擎,它让开发者可以将他们的应用及其依赖打包到一个可移植的镜像中,然后发布到任何流行的Linux或Windows操作系统的机器上,也可以实现虚拟化。容器是完全使用沙箱机制,相互之…
使用numpy处理图片——90度旋转
在《使用numpy处理图片——镜像翻转和旋转》一文中,我们介绍了如何将图片旋转的方法。本文将使用更简单的方法旋转图片90度。
左旋转90度
import numpy as np
import PIL.Image as Imagedata np.array(Image.open(the_starry_night.jpg))# left 90
rot90LeftWith…
详细分析Java中的分布式任务调度框架 XXL-Job
目录 前言1. 基本知识2. Demo3. 实战 前言
可视化任务调度 可视化配置
1. 基本知识
在Java中,分布式任务调度框架 XXL-Job 是一个开源的分布式任务调度平台,用于实现分布式系统中的定时任务调度和分布式任务执行。
下面是关于XXL-Job的一些概念、功…
Java lambda表达式如何自定义一个toList Collector
匿名类:
package l8;import java.util.*;
import java.util.function.BiConsumer;
import java.util.function.BinaryOperator;
import java.util.function.Function;
import java.util.function.Supplier;
import java.util.stream.Collector;
import java.util.s…
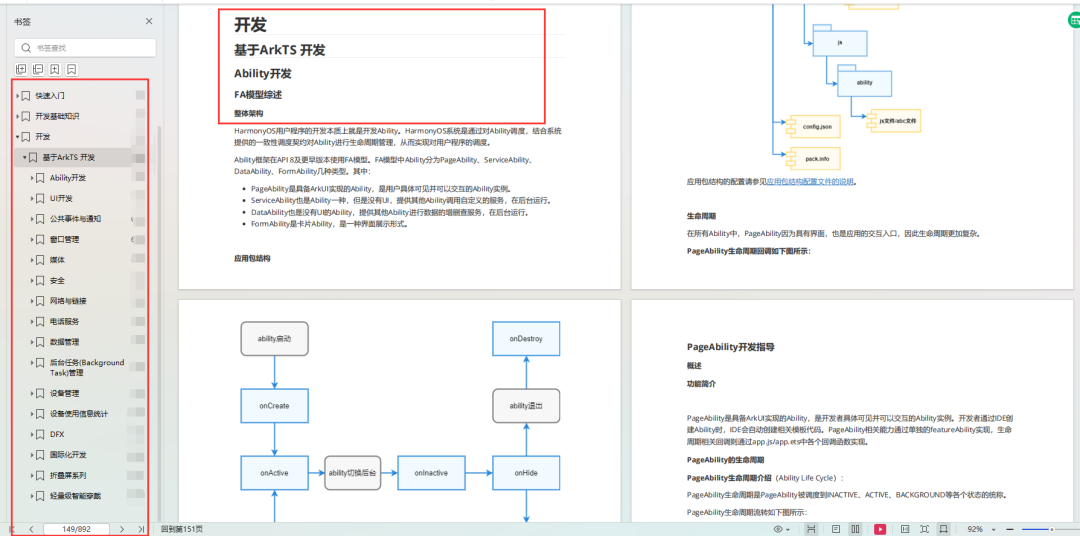
OpenHarmony—开发环境搭建
背景
因为没有实体的开发硬件,且不想破坏原有的Linux环境,所以这里基于 Docker QEMU 搭建开发环境
宿主机Linux系统命令行方式DockerQEMU 6.2
Docker环境准备
安装Docker
在Ubuntu中,可以使用下面的命令来安装Docker: sudo …
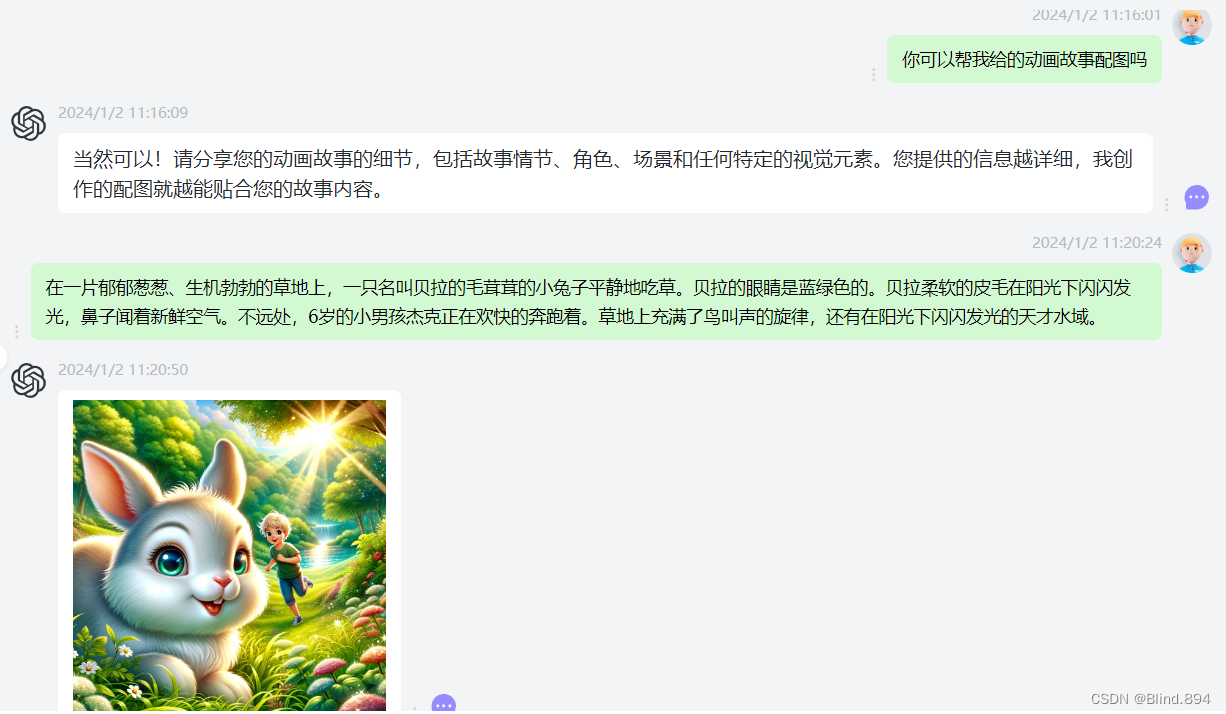
GPT-4与DALL·E 3:跨界融合,开启绘画与文本的新纪元
在人工智能的发展浪潮中,MidTool(https://www.aimidtool.com/)的GPT-4与DALLE 3的集成代表了一个跨越式的进步。这一集成不仅仅是技术的结合,更是艺术与文字的完美融合,它为创意产业带来了革命性的变革。本文将探讨GPT…
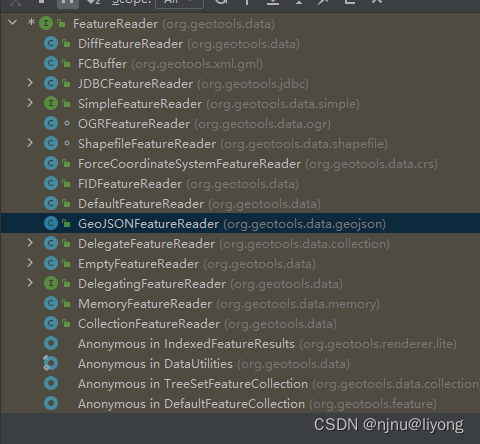
Geotools-PG空间库(Crud,属性查询,空间查询)
建立连接
经过测试,这套连接逻辑除了支持纯PG以外,也支持人大金仓,凡是套壳PG的都可以尝试一下。我这里的测试环境是Geosence创建的pg SDE,数据库选用的是人大金仓。
/*** 获取数据库连接资源** param connectConfig* return* {…
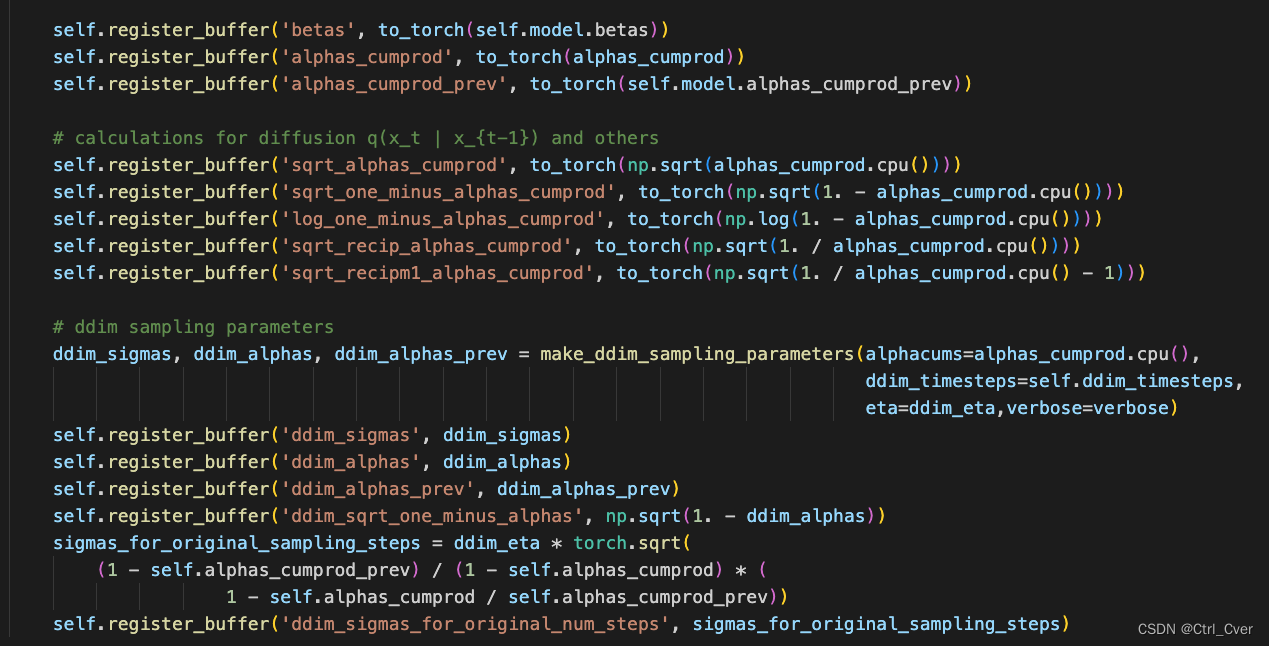
stable diffusion代码学习笔记
前言:本文没有太多公式推理,只有一些简单的公式,以及公式和代码的对应关系。本文仅做个人学习笔记,如有理解错误的地方,请指出。
资源
本文学习的代码;相关文献:
Denoising Diffusion Probab…
使用Sqoop将数据导入Hadoop的详细教程
在大数据处理中,Sqoop是一个强大的工具,它可以将关系型数据库中的数据导入到Hadoop生态系统中,以便进行进一步的分析和处理。本文将提供一个详细的教程,以帮助大家了解如何使用Sqoop将数据导入Hadoop。
准备工作
在开始之前&…
银河麒麟v10安装前端环境(Node、vue、Electron+vite)
此帖子所提到的所有依赖包都是基于银河麒麟v10真机的arm架构包,如果是在windows上的虚拟机上 把依赖包换成x64的包即可,方法步骤都是一样
一.node安装
原始方法安装(建议用第二种nvm方法,因为更简单):
1…
性能优化-OpenMP概述(一)-宏观全面理解OpenMP
本文旨在从宏观角度来介绍OpenMP的原理、编程模型、以及在各个领域的应用、使用、希望读者能够从本文整体上了解OpenMP。 🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能(HPC)开发基础…
Open CV 图像处理基础:(五)Java 使用 Open CV 的绘图函数
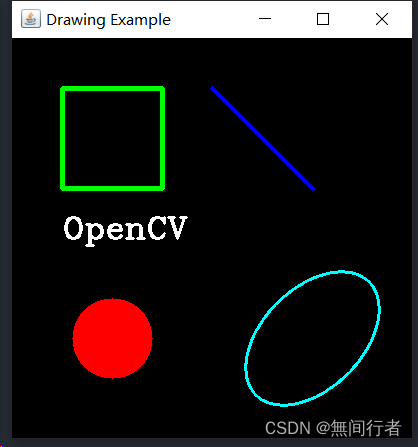
Java 使用 Open CV 的绘图函数
使用 Open CV 在 Java 中对图片使用绘图函数,分别绘制矩形、斜线、圆形、椭圆形以及添加文本 Java 使用 Open CV 的绘图函数 Java 使用 Open CV 的绘图函数函数绘制矩形绘制线绘制圆形绘制椭圆添加文本 代码示例Open CV 专栏导航 函…
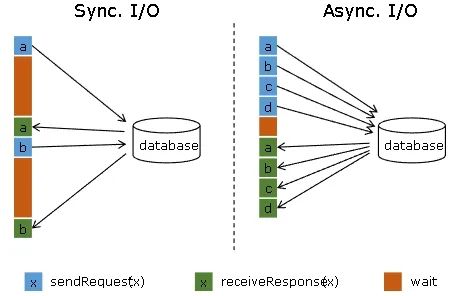
NLP(十八):LLM 的推理优化技术纵览
原文:NLP(十八):LLM 的推理优化技术纵览 - 知乎
目录
收起
一、子图融合(subgraph fusion)
1.1 FasterTransformer by NVIDIA
1.2 DeepSpeed Inference by Microsoft
1.3 MLC LLM by TVM
二、模型压…
面试算法115:重建序列
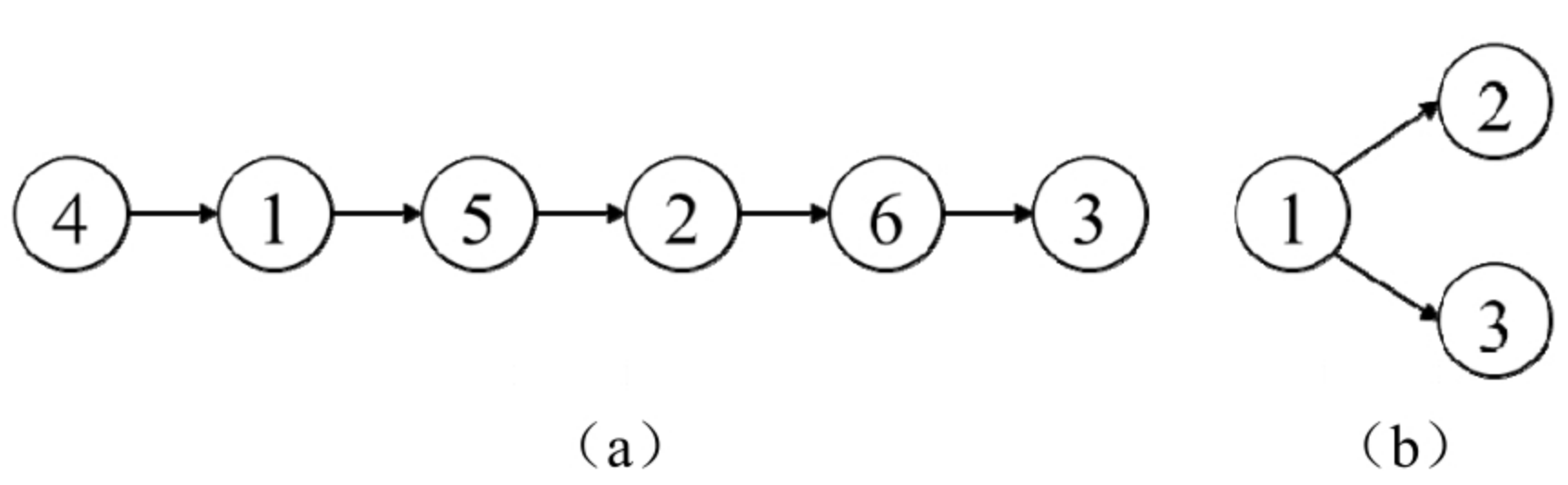
题目
长度为n的数组org是数字1~n的一个排列,seqs是若干序列,请判断数组org是否为可以由seqs重建的唯一序列。重建的序列是指seqs所有序列的最短公共超序列,即seqs中的任意序列都是该序列的子序列。 例如,如果数组org为…
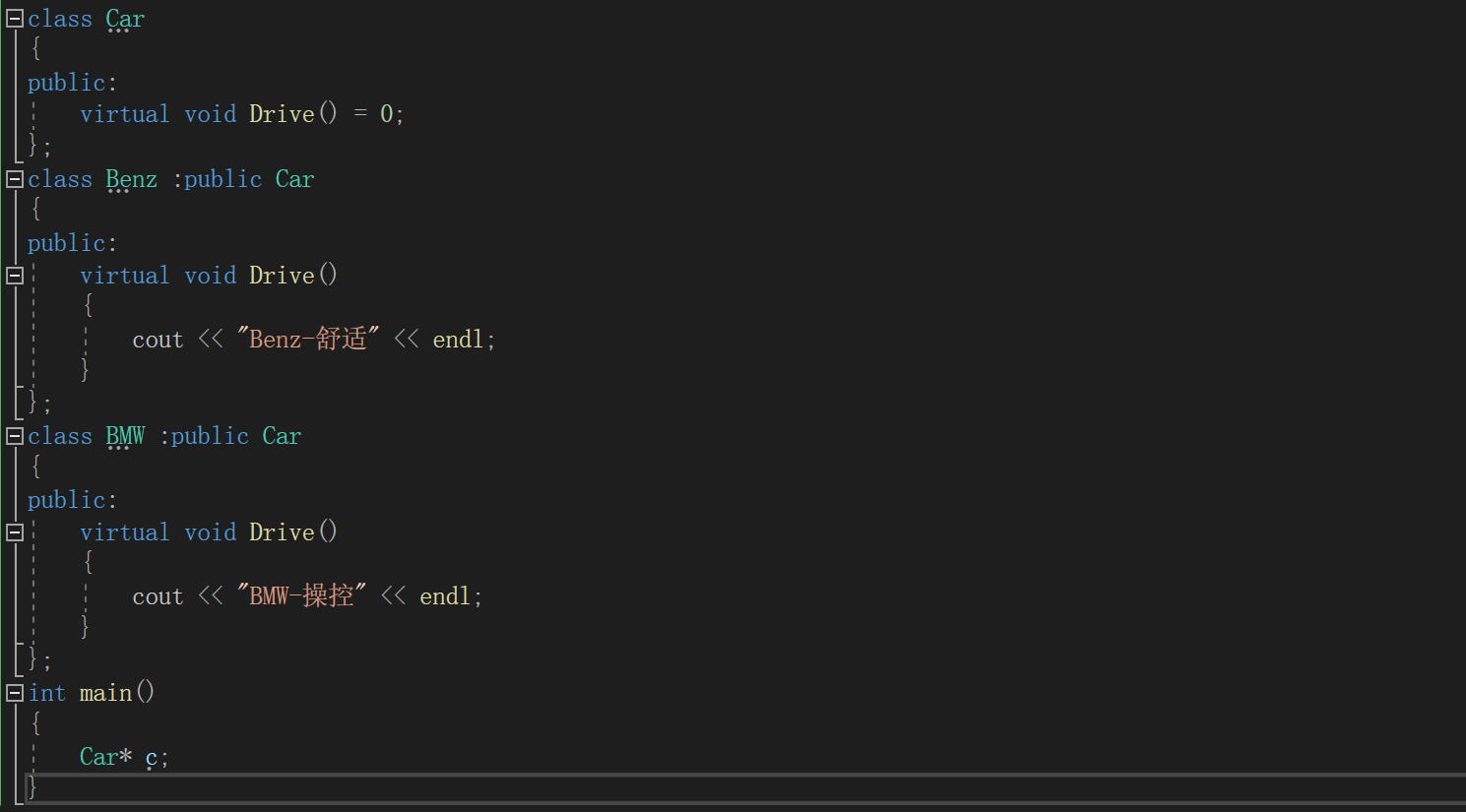
C++进阶(三)多态
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、多态的概念1、概念 二、多态的定义及实现1、多态的构成条件2、虚函数3、虚函数的重写4、C…