本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/311164.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
麒麟操作系统缓存rpm包,制作离线yum源
缓存rpm包,以make为例
mkdir -p /data/yum
yumdownloader --resolve --destdir/data/yum make制作离线yum包
yum install createrepo -y
cd /data/yum
createrepo .写yum配置文件/etc/yum.repos.d/local.repo
[local-repo]
namelocal-repo
baseurlfile:///data/…
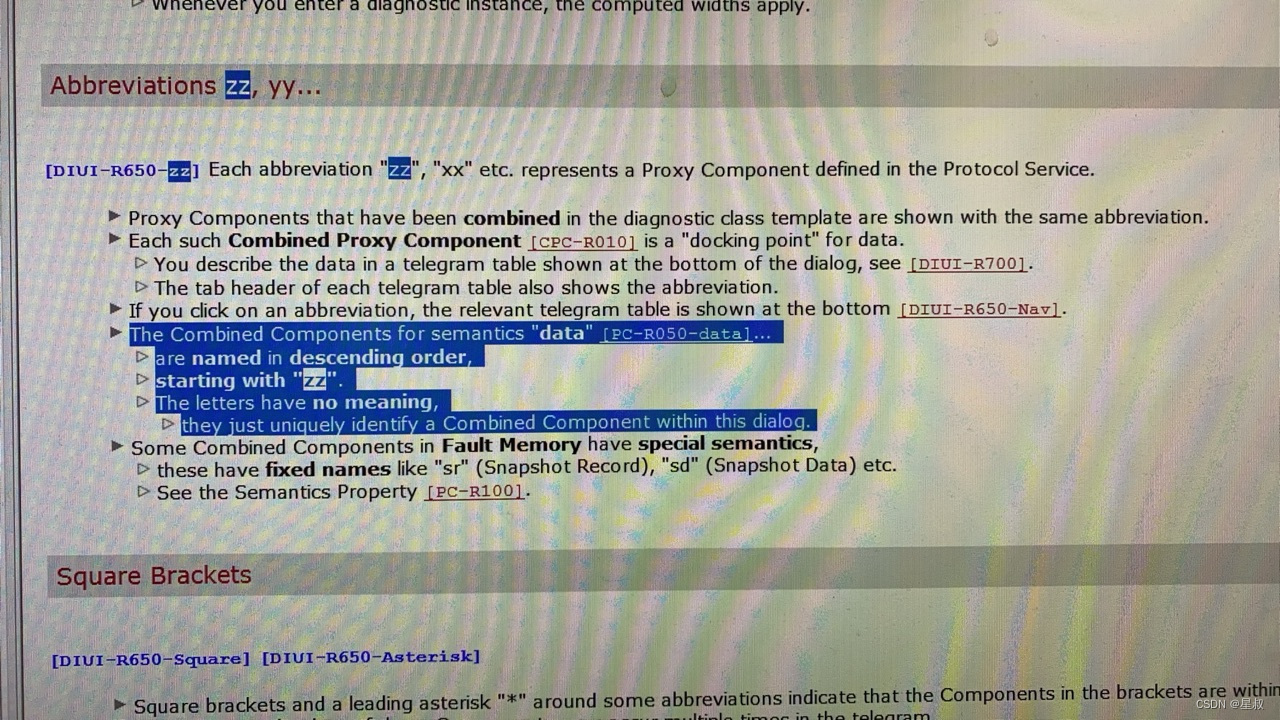
Cdd诊断数据控中的zz rc yy
如上图所示的Cdd Candela Diagnostic Descriptions 诊断数据库会话定义中有许多的标识符缩写,如zz rc LL xx 等 其实这些字母没有意义,它们只是唯一地标识对话框中的组合组件。
Github上传代码/删除仓库/新建分支的操作流程记录
首先先安装git,安装完git后,看如下操作指令:
输入自己的用户名和邮箱(为注册GITHUB账号时的用户名和邮箱): git config --global user.name "HJX-exoskeleton" git config --global user.email …
Mysql事务的处理
1、事务,就是一组命令的操作。 不过这一组命令,我们有时候需要使用手动提交; 1、使用这组命令可以查询出来现在的提交方式:自动提交(就是命令输入,点击enter后,会不会直接对表格产生修改&#x…
深入理解Spring IOC
1. IOC 理论
IOC 全称控制反转,英文名为 Inversion of Control,它还有一个别名为 DI(Dependency Injection),即依赖注入。
在我们刚接触Spring的时候,我们就听说了IOC,但是对于IOC的理解,貌似…
对快速排序思想的进一步理解,分而治之,欧几里得算法(常用求最大公约数的方法)
自己找到的最优的快排的代码
快速排序 思想 分而治之使用欧几里得算法(辗转相除法)来求解一个应用题 假设有一块地,现在用这个同样大小的正方形来铺满,求所可用的最大的正方形地砖的面积 这两个方法放在一起是因为这个欧几里得要…
Spring Security入门
目录
1.简介
与shiro对比
添加依赖
执行流程
2.UserDetailsService
User实现类
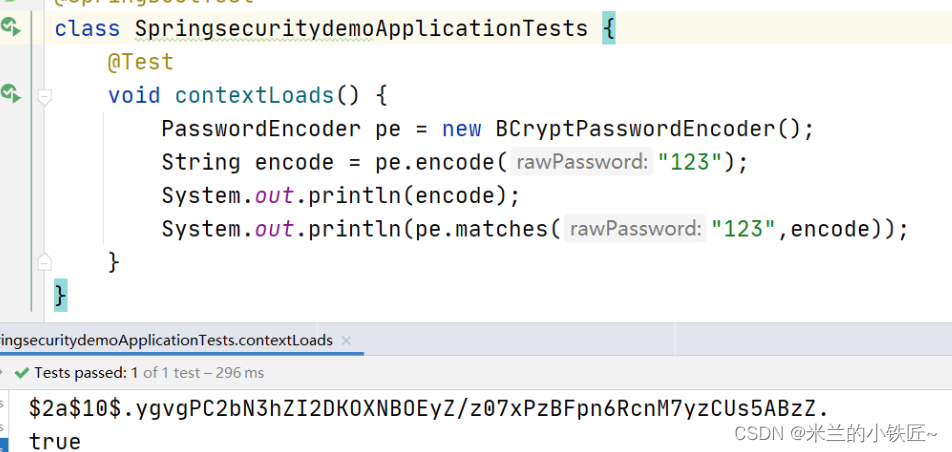
3.PasswordEncoder
BCryptPasswordEncoder
4.自定义登录逻辑
5.自定义登录界面
6.设置请求账户和密码的参数
7.自定义登陆处理器
成功
失败
8.判断
权限判断
角色判断
…
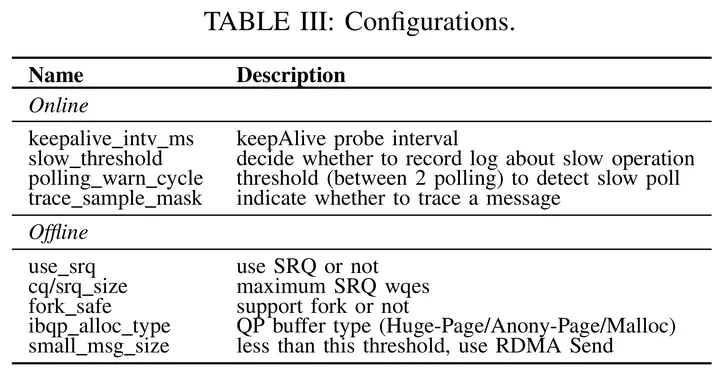
阿里云RDMA通信库XRDMA论文详解
RDMA(remote direct memory access)即远端直接内存访问,是一种高性能网络通信技术,具有高带宽、低延迟、无CPU消耗等优点。RDMA相比TCP在性能方面有明显的优势,但在编程复杂度上RDMA verbs却比TCP socket复杂一个数量级。
开源社区和各大云厂…
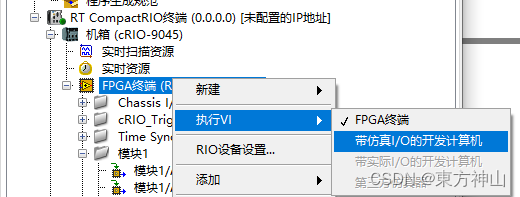
【LabVIEW FPGA入门】没有CompactRIO时进行编程测试
1.新建一个空白项目。 2.新建cRIO终端。 要添加仿真的远程实时目标,请选择项目名称,右击并选择新建>>目标和设备(Targets and Devices)。 3.新建终端和设备,选一个cRIO型号 接下来,当添加目标和设备窗口出现时,请…
Gauss消去法(C++)
文章目录 算法描述顺序Gauss消去法列选主元Gauss消去法全选主元Gauss消去法Gauss-Jordan消去法 算法实现顺序Gauss消去法列选主元Gauss消去法全选主元Gauss消去法列选主元Gauss-Jordan消去法 实例分析 Gauss消去法是求解线性方程组较为有效的方法, 它主要包括两个操作, 即消元和…
nginx(1.13.7)首次安装出现:【make: *** 没有规则可以创建“default”需要的目标“build” 问题】解决措施
目录 前言:
一.龙蜥(Anolis)操作系统上安装GCC
1.安装gcc
2.检验安装
二.安装出现 make: *** 没有规则可以创建“default”需要的目标“build” 问题
1.解压安装nginx 2.安装出现问题展示 3.解决措施
4.重新编译进行安装
5…
UCB Data100:数据科学的原理和技巧:第十三章到第十五章
十三、梯度下降 原文:Gradient Descent 译者:飞龙 协议:CC BY-NC-SA 4.0 学习成果 优化复杂模型 识别直接微积分或几何论证无法帮助解决损失函数的情况 应用梯度下降进行数值优化
到目前为止,我们已经非常熟悉选择模型和相应损…
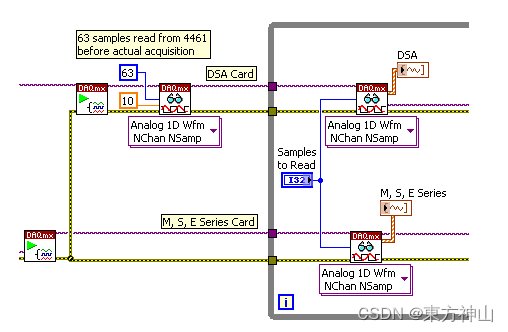
【NI-DAQmx入门】LabVIEW中DAQmx同步
1.同步解释
1.1 同步基础概念 触发器:触发器是控制采集的命令。您可以使用触发器来启动、停止或暂停采集。触发信号可以源自软件或硬件源。 时钟:时钟是用于对数据采集计时的周期性数字信号。根据具体情况,您可以使用时钟信号直接控制数据采…
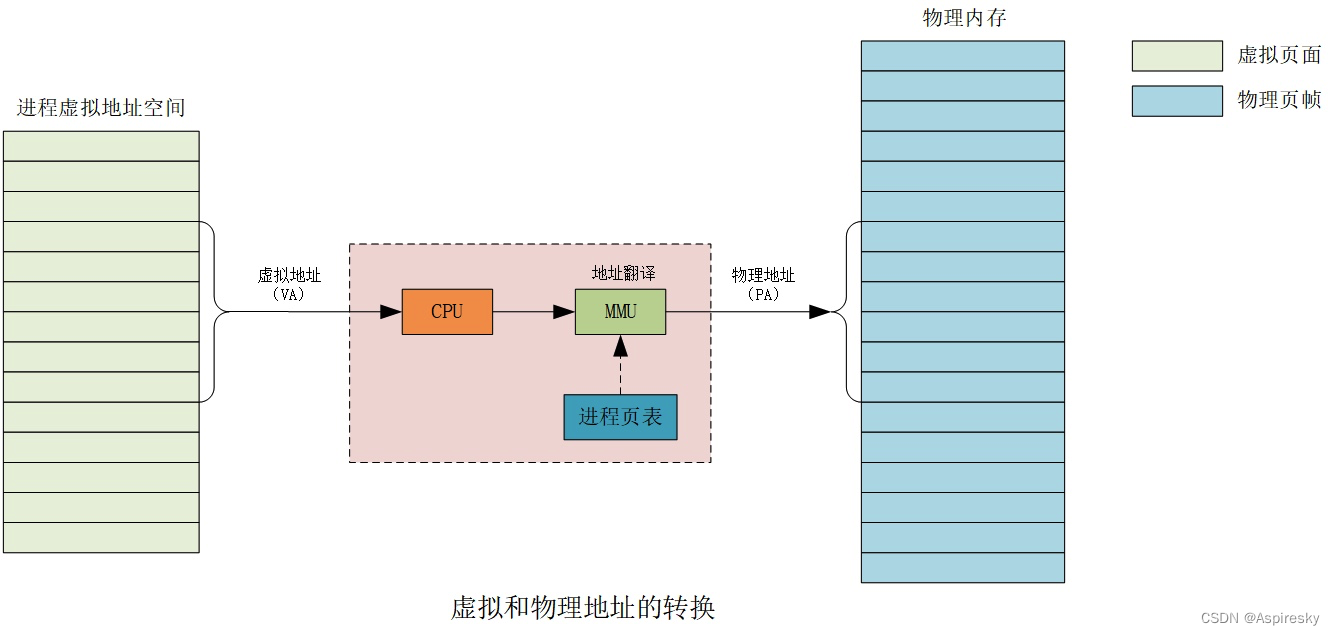
浅析Linux进程地址空间
前言
现代处理器基本都支持虚拟内存管理,在开启虚存管理时,程序只能访问到虚拟地址,处理器的内存管理单元(MMU)会自动完成虚拟地址到物理地址的转换。基于虚拟内存机制,操作系统可以为每个运行中的进程创建…
[足式机器人]Part2 Dr. CAN学习笔记 - Ch03 傅里叶级数与变换
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-Ch03 傅里叶级数与变换 1. 三角函数的正交性2. 周期为 2 π 2\pi 2π的函数展开为傅里叶级数3. 周期为 2 L 2L 2L的函数展开4. 傅里叶级数的复数形式5. 从傅里叶级数推导傅里叶变换FT6. 总结 1. …
C语言如何提高程序的可读性?
一、问题 可读性是评价程序质量的一个重要标准,直接影响到程序的修改和后期维护,那么如何提高程序的可读性呢?
二、解答
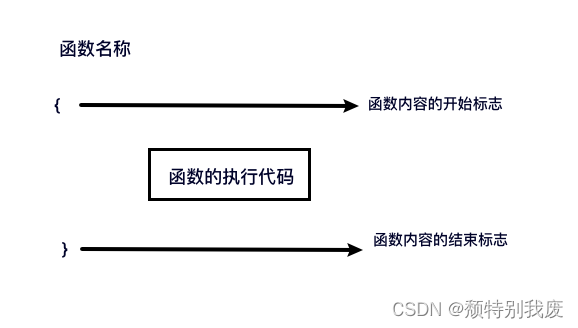
提高程序可读性可以从以下几方面来进行。 (1)C程序整体由函数构成的。 程序中,main()就是其中…
备战抖音商城好物年货节,品牌焕发新商机
农历春节前的最后一个月,打工人们逐渐将置办年货提上日程。忙碌了一年的辛苦与疲惫,总能在喜气洋洋买年货的过程中,被一扫而空。这是“年味”的开始,也是公司高管郭广宇面临的一场关键战役。 郭广宇今年35岁,是三只松鼠…







![[足式机器人]Part2 Dr. CAN学习笔记 - Ch03 傅里叶级数与变换](https://img-blog.csdnimg.cn/direct/9675ebcd1f6d4f81820824dfea2fb2aa.png)