本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/326313.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
C语言练习题110例(十)
91.杨辉三角
题目描述:
KK知道什么叫杨辉三角之后对杨辉三角产生了浓厚的兴趣,他想知道杨辉三角的前n行,请编程帮他
解答。杨辉三角,本质上是二项式(ab)的n次方展开后各项的系数排成的三角形。其性质包括:每行的端点数为1&…
uniapp canvas做的刮刮乐解决蒙层能自定义图片
最近给湖南中烟做元春活动,一个月要开发4个小活动,这个是其中一个难度一般,最难的是一个类似鲤鱼跃龙门的小游戏,哎,真实为难我这个“拍黄片”的。下面是主要代码。 <canvas :style"{width:widthpx,height:hei…
区块链技术在教育领域的应用:Web3教育变革
随着Web3时代的来临,区块链技术在各个领域都展现出了巨大的潜力,而在教育领域,区块链的应用正引领着一场教育变革。本文将深入探讨区块链技术在教育领域的创新应用,以及这一应用如何推动Web3时代的教育变革。 1. 学历和成绩的去中…
【数学笔记】一元n次不等式,分式不等式,绝对值不等式
不等式 基本性质 一元n次不等式一元二次不等式一元高次不等式分式不等式绝对值不等式 基本性质
性质 a > b ⇔ b < a a>b\Leftrightarrow b<a a>b⇔b<a a > b , b > c ⇒ a > c a>b,b>c\Rightarrow a>c a>b,b>c⇒a>c a > b ,…
Raspbian安装云台
Raspbian安装云台 1. 源由2. 选型3. 组装4. 调试4.1 python3-print问题4.2 python函数入参类型错误4.3 缺少mjpg-streamer可执行文件4.4 缺失编译头文件和库4.5 python库缺失4.6 图像无法显示,但libcamera-jpeg测试正常4.7 异常IOCTL报错4.8 Git问题 5. 效果5.1 WEB…
linux conda 配置 stable video diffusion
安装教程
1 下载仓库源码
git clone https://github.com/Stability-AI/generative-models.git2 创建conda环境
conda create -n svd python3.10
conda activate svd3 安装pytorch gpu
cuda和cudnn请参考其他链接配置,使用 conda 或者 pip 安装 pytorch
# 使用c…
Dockerfile里ADD * 保留原来的目录结构
1、问题
给新模块写Dockerfile,很多静态资源分散在各个目录,于是Dockerfile里我直接一句:
ADD ./* /dest/镜像出来后,启动容器,进入容器种后发现:文件拷贝成功,但原来的目录结构都不在了&…
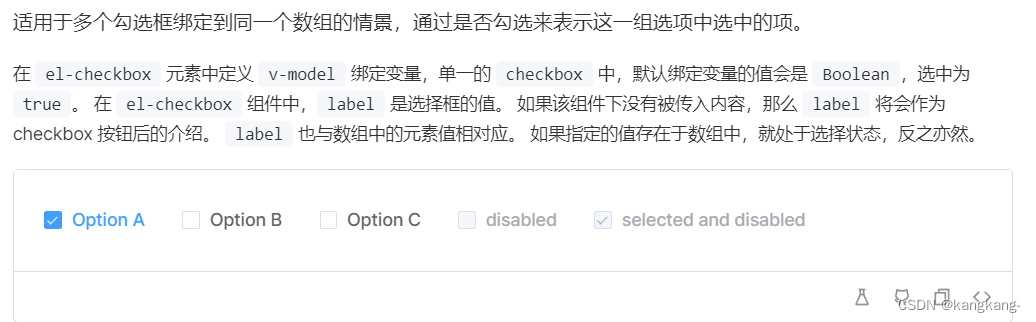
Vue3+ElementUI 多选框中复选框和名字点击方法效果分离
现在的需求为 比如我点击了Option A ,触发点击Option A的方法,并且复选框不会取消勾选,分离的方法。 <el-checkbox-group v-model"mapWork.model_checkArray.value">
<div class"naipTypeDom" v-for"item …
蓝桥杯---三羊献瑞
观察下面的加法算式: 其中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。
请你填写“三羊献瑞”所代表的4位数字(答案唯一),不要填写任何多余内容。
答案 代码
public class _03三羊献瑞 {public static void main(String[] args) {//c 生 b 瑞 g 献 d 辉…
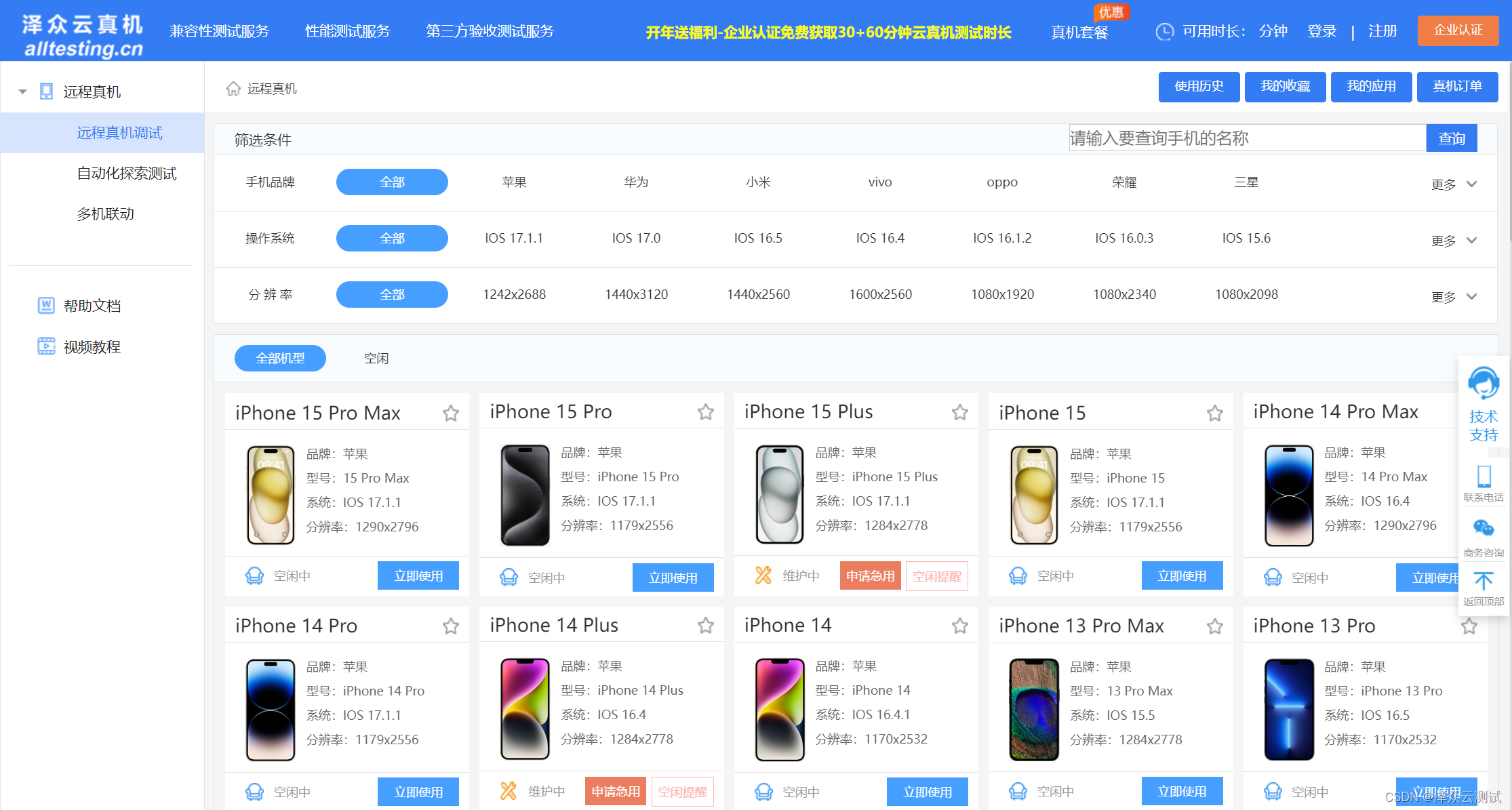
泽众云真机-机型集中化运维方案升级全面完成
2024年元月份,泽众云真机运维团队,经过几个月软硬件多轮安装调试,机型集中化运维方案升级全面完成。解决了云真机的机型集中化运维难题,方便了运营人员手机管理。 具体如下:
1、集中化运维,如服务器、PC、…
电脑文件mfc140.dll丢失的解决方法指导,怎么快速修复mfc140.dll
mfc140.dll 文件的缺失是个普遍的问题,在日常使用中可能会时不时遇到。本文主要目的是详细介绍一旦遇到 mfc140.dll 文件缺失,应该如何进行下载和安装的步骤。不再赘言,下面就一起深入了解mfc140.dll丢失的解决方法指导。 一. mfc140.dll的作…
【操作系统】实验九 写一个设备驱动程序
🕺作者: 主页 我的专栏C语言从0到1探秘C数据结构从0到1探秘Linux 😘欢迎关注:👍点赞🙌收藏✍️留言 🏇码字不易,你的👍点赞🙌收藏❤️关注对我真的很重要&…
一、Lamdba 表达式与函数式接口(最终版)
一、Lamdba 表达式与函数式接口
1.1 Lamdba 表达式与函数式接口
1.1.1 Lambda 表达式概述
Lambda 表达式是 Java 8 引入的一个新特性Lambda 表达式可以被视为匿名函数允许在需要函数的地方以更简洁的方法定义功能Lambda 表达式可以完成简洁的函数定义Stream API 中大量使用了…
ISO27001认证:企业与个人发展的必备之选
ISO27001认证,对于企业和个人来说,都具有极高的价值和重要性。作为国际权威的信息安全管理体系标准,它为企业提供了保障信息安全、防范风险和提升竞争力的有力工具。 💼对企业的价值: ISO27001认证可以帮助企业满足国家…
编曲学习:识谱、节奏时值、音符输入
34届课程体系介绍 作业体系介绍 识谱、节奏时值 音符输入https://app8epdhy0u9502.pc.xiaoe-tech.com/live_pc/l_65ab7dcee4b04c10a12461ab?course_idcourse_2XLKtQnQx9GrQHac7OPmHD9tqbv
找到钢琴中的中央C 12个键为1组! 小字一组第1个音是中央C!
钢…
Linux抽象文件系统
一.概念
Linux采用了抽象文件系统的概念来统一管理不同类型的文件和文件系统。抽象文件系统是对不同文件系统的封装,使得用户和应用程序可以以相同的方式访问和操作不同类型的文件系统。
Linux的抽象文件系统通过以下几个组件来实现: VFS(V…
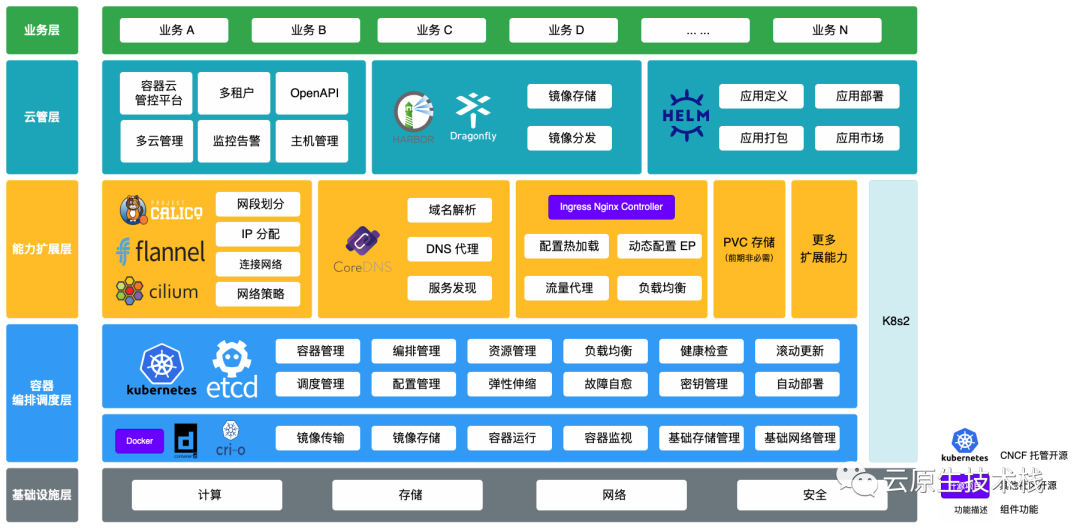
基于Kubernetes(K8s)构建企业容器云基础运行环境
cncfstack 新 文章上线: 书名:《云原生解决方案》 地址:https://zhaowenyu.com/cncf-solution 访问:文章底部“阅读原文”或访问域名 云原生计算是云计算发展新的里程碑阶段,是当今与未来很长一段时间中 IT 发展的技…
2024年PMP备考学习资料整合汇总!!
你是否也有过类似的经历? 为了获取备考资料,有的同学在论坛、知乎或者相关垂直类网站下载了很多的资料,这些资料大部分是机构进行获客引流的资料,没有真正的干货。 经常会看到10G、20G的资料包,感觉内容很丰富…
一、Kotlin 开发环境搭建
1. Kotlin 官网
https://kotlinlang.org/
2. Kotlin 命令行工具下载 下载网址: https://github.com/JetBrains/kotlin/releases/tag/v1.3.50 切换其他版本,改下版本号即可 下载 kotlin-compiler-1.3.50.zip 文件即可 解压 kotlin-compiler-1.3.50.zip…
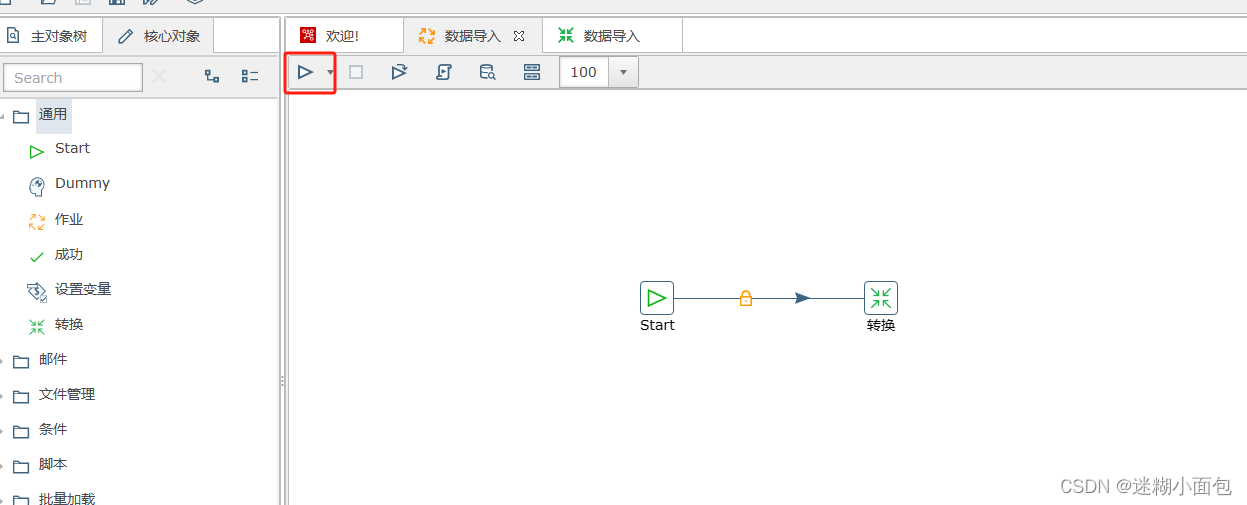
Kettle-Docker部署+Sqlserver数据同步Mysql+Start定时任务
一. 背景介绍
1. ETL是什么 ETL(Extract-Transform-Load),即数据抽取、转换、装载的过程。它是一种思想,主要是说,从不同的数据源获取数据,并通过对数据进行处理(格式,协议等转换&a…