本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/361377.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
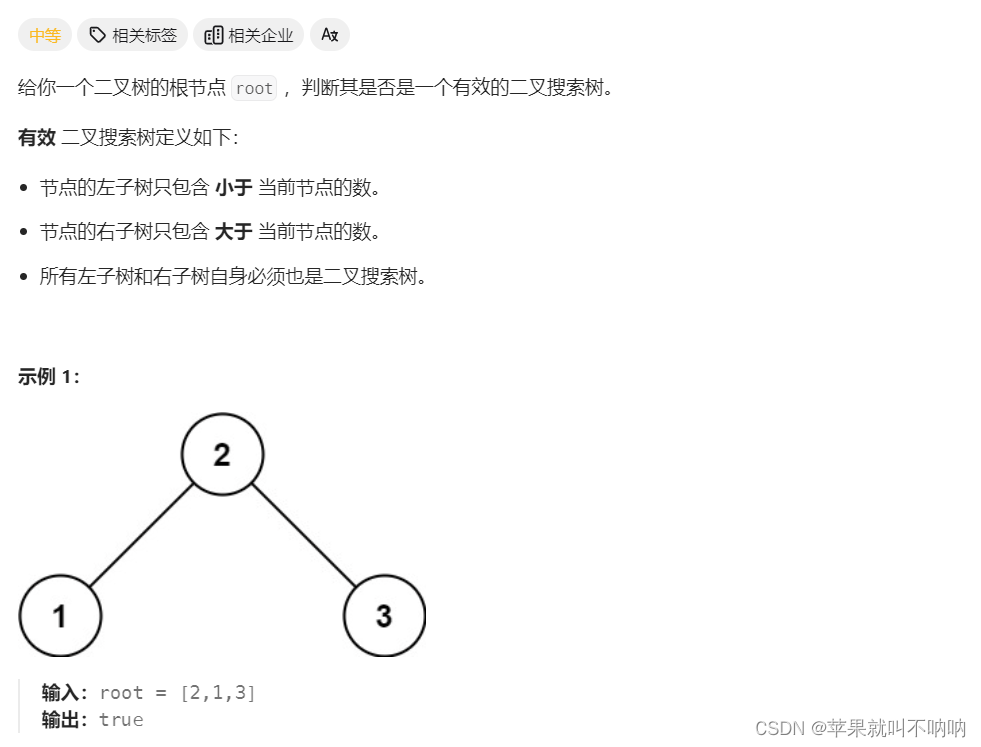
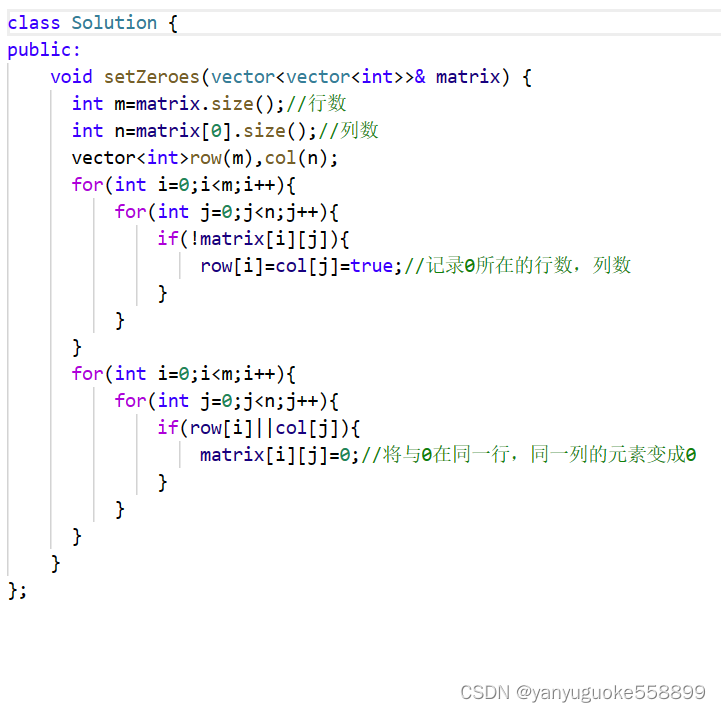
★【二叉搜索树(中序遍历特性)】【 ★递归+双指针】Leetcode 98. 验证二叉搜索树
★【二叉搜索树(中序遍历特性)】【 ★递归双指针】Leetcode 98. 验证二叉搜索树 二叉搜索树 98. 验证二叉搜索树解法1 笨 中序递归遍历为一个数组 然后判断数组是不是升序排列就可以★解法2 不使用数组 递归法 ---------------🎈Ἰ…
利用IP地址识别风险用户:保护网络安全的重要手段
随着互联网的发展和普及,网络安全问题日益突出,各种网络诈骗、恶意攻击等风险不断涌现,给个人和企业的财产安全和信息安全带来了严重威胁。在这样的背景下,利用IP地址识别风险用户成为了保护网络安全的重要手段之一。IP数据云探讨…
关于vue中关于eslint报错的问题
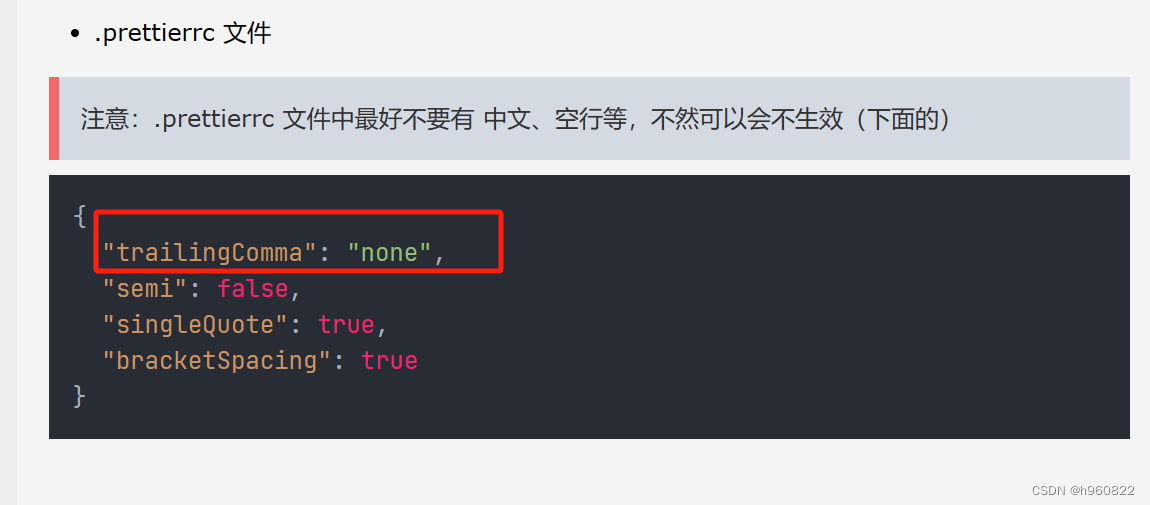
1 代码保存的时候会自动将单引号报错为双引号 导致eslint报错的问题, 解决思路: 在项目根目录下新建一个.prettierrc.json文件
{
“tabWidth”: 2,“useTabs”: false,“singleQuote”: true,“semi”: false}
2 关于报错代码的时候 出现尾随逗号报错…
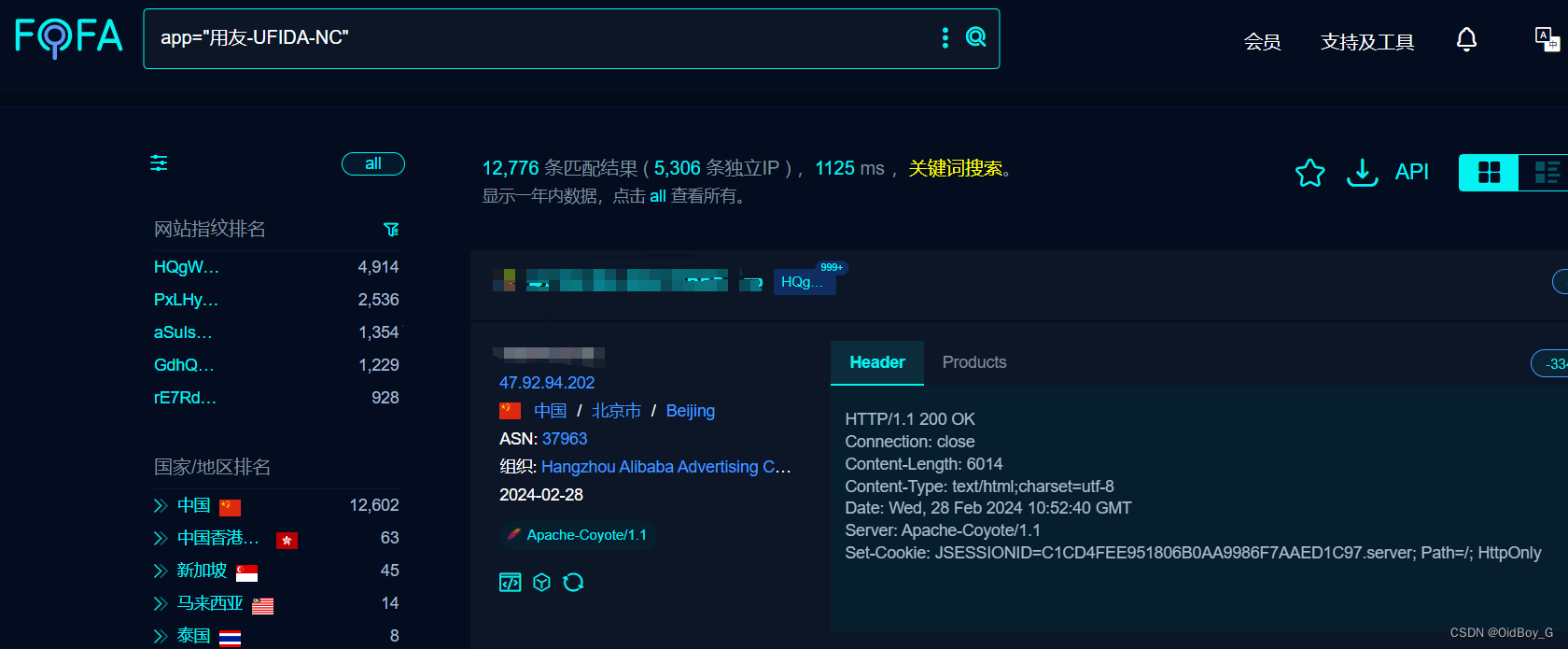
用友 NC 23处接口XML实体注入漏洞复现
0x01 产品简介
用友 NC 是用友网络科技股份有限公司开发的一款大型企业数字化平台。
0x02 漏洞概述
用友 NC 多处接口存在XML实体注入漏洞,未经身份验证攻击者可通过该漏洞读取系统重要文件(如数据库配置文件、系统配置文件)、数据库配置文件等等,导致网站处于极度不安全…
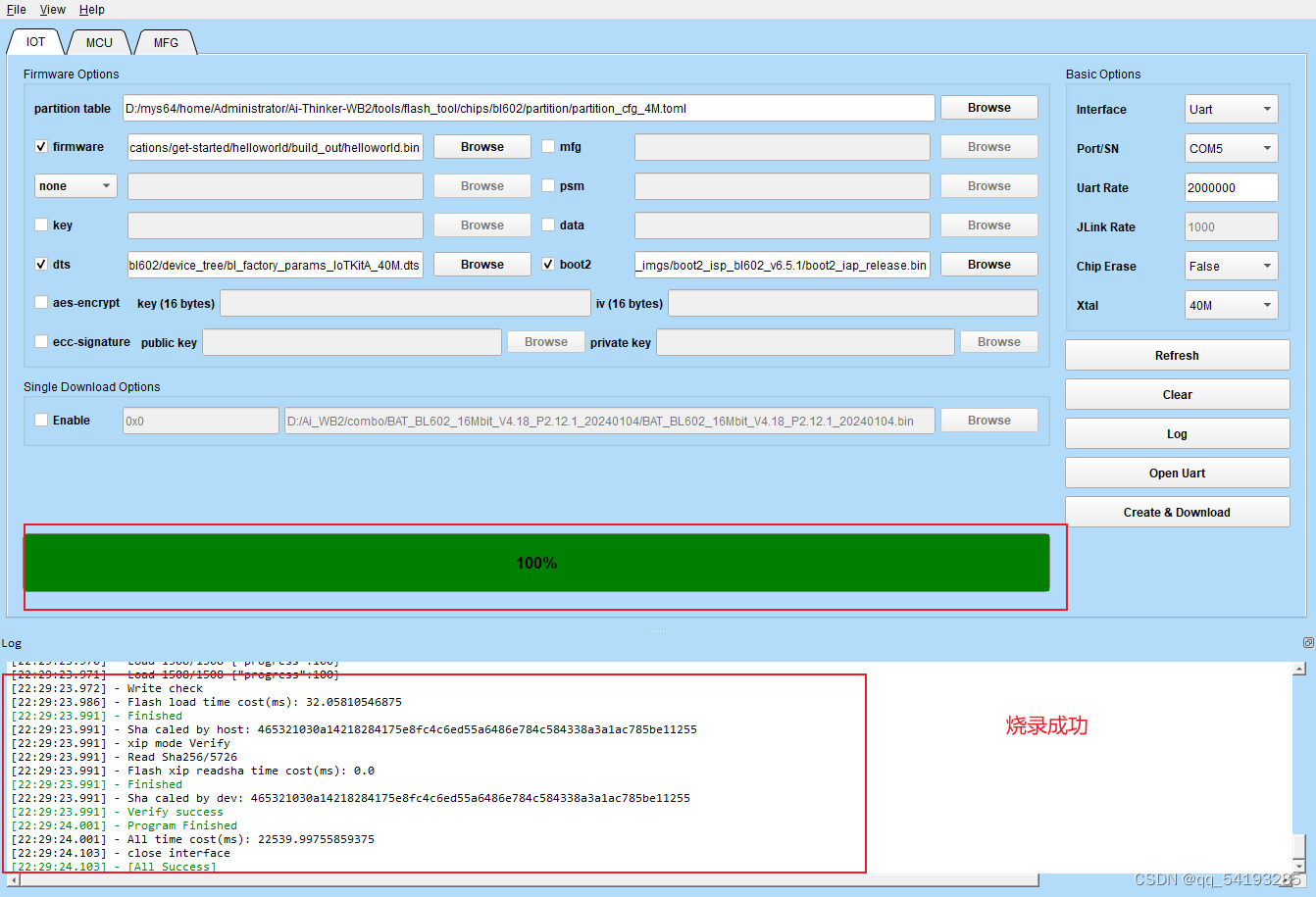
Ai-WB2-32S在window下使用vs 和 msys2编译以及烧录
文章目录 前言一、使用前准备第一步 安装vscode第二步 安装msys2 二、使用步骤1.打开MSYS2 MINGW64(1)在开始栏中找到MSYS2 MINGW64并打开(2)安装git(3)安装make(4)安装好之后的文件…
港大提出GraphEdit, 图数据编辑大模型!
论文链接:https://arxiv.org/abs/2402.15183 代码链接:https://github.com/HKUDS/GraphEdit
摘要
图结构学习(Graph Structure Learning, GSL)旨在通过生成新的图结构来捕捉图结构数据中节点之间的内在依赖性和交互关系。
图神…
WSL2外部网络设置
1 关闭所有WSL系统 wsl --shutdown 2 打开Hyper-V管理器 3 将“虚拟交换机管理器”-> ”WSL连接类型“设置为“外部网络” 4 启动WSL系统,手动修改WSL网络 将WSL网络IP修改为192.168.1.9 sudo ip addr del $(ip addr show eth0 | grep inet\b | awk {print $2} |…
YOLOv9有效提点|加入SE、CBAM、ECA、SimAM等几十种注意力机制(一)
专栏介绍:YOLOv9改进系列 | 包含深度学习最新创新,主力高效涨点!!! 一、本文介绍 本文将以SE注意力机制为例,演示如何在YOLOv9种添加注意力机制! 《Squeeze-and-Excitation Networks》 SENet提出…
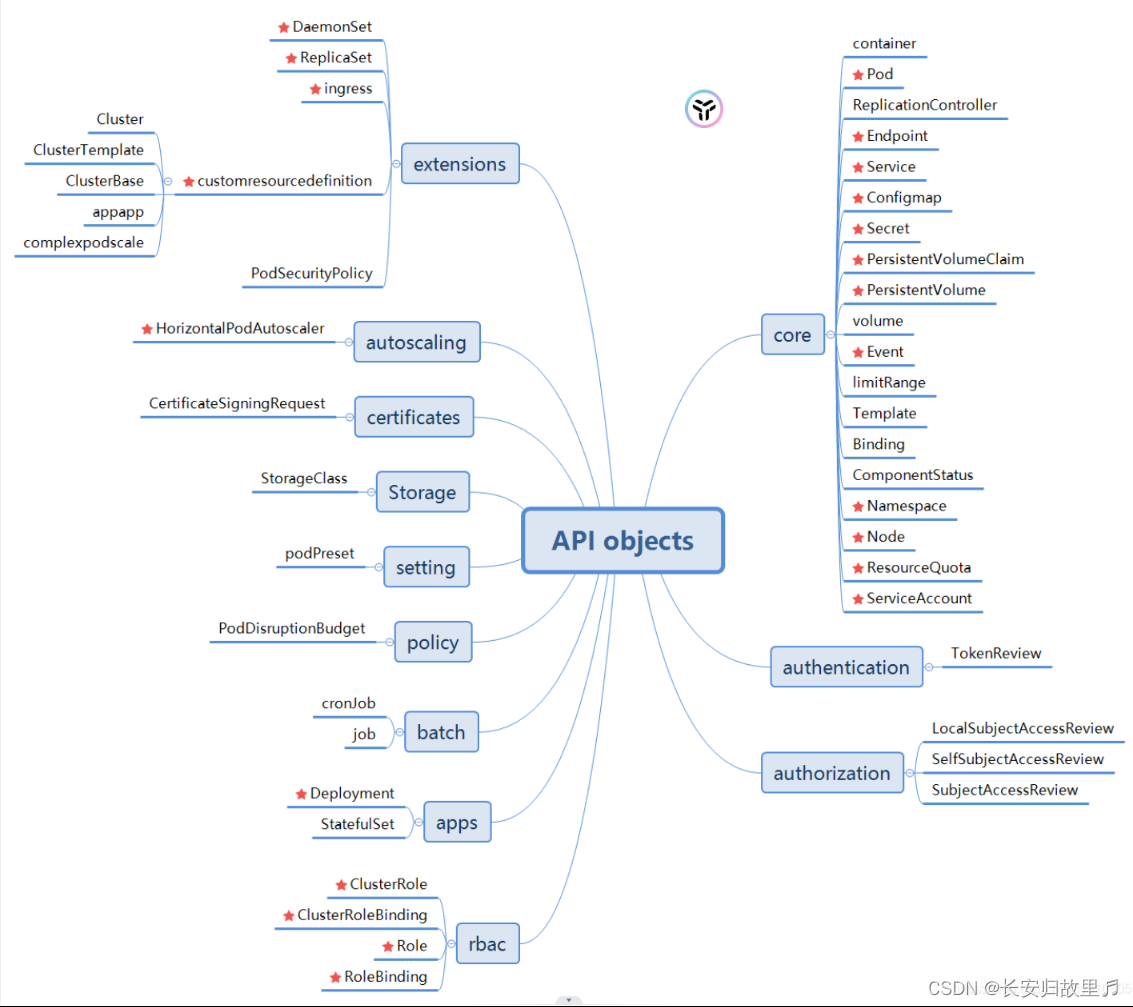
【k8s相关资源api操作】
k8s相关资源api操作 文章目录 k8s相关资源api操作AdmissionregistrationApiextensionApiregistrationAppsV1ApiAutoscalingV1ApiBatchV1ApiCertificatesApi 证书相关CoordinationV1Api 最重要的CoreV1Api !!!CustomObjectsApiDiscoveryV1ApiEventsV1ApiFlowcontrolApiserverApi…
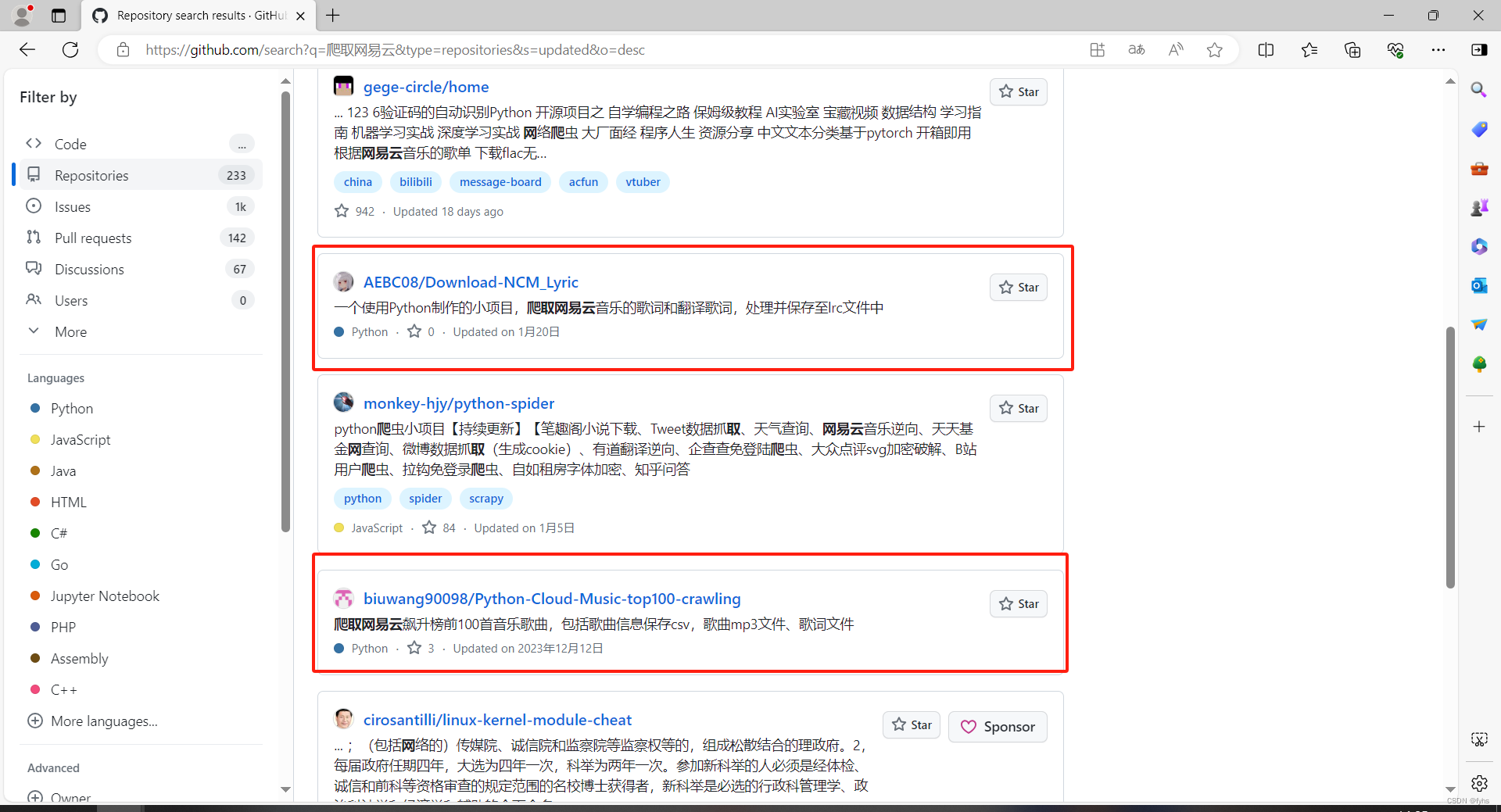
通过GitHub探索Python爬虫技术
1.检索爬取内容案例。 2.找到最近更新的。(最新一般都可以直接运行) 3.选择适合自己的项目,目前测试下面画红圈的是可行的。 4.方便大家查看就把代码粘贴出来了。
#图中画圈一代码
import requests
import os
import rewhile True:music_id input("请输入歌曲…
Dell R730 2U服务器实践3:安装英伟达上代专业AI训练Nvidia P4计算卡
Dell R730是一款非常流行的服务器,2U的机箱可以放入两张显卡,这次先用一张英伟达上代专业级AI训练卡:P4卡做实验,本文记录安装过程。 简洁步骤: 打开机箱将P4显卡插在4号槽位关闭机箱安装驱动 详细步骤:
对…
重拾前端基础知识:CSS
重拾前端基础知识:CSS 前言选择器简单选择器属性选择器组合选择器 插入CSS内嵌样式(Inline Style)内部样式(Internal Style)外部样式(External Style) 层叠颜色背景颜色文本颜色RGB 颜色HEX 颜色…
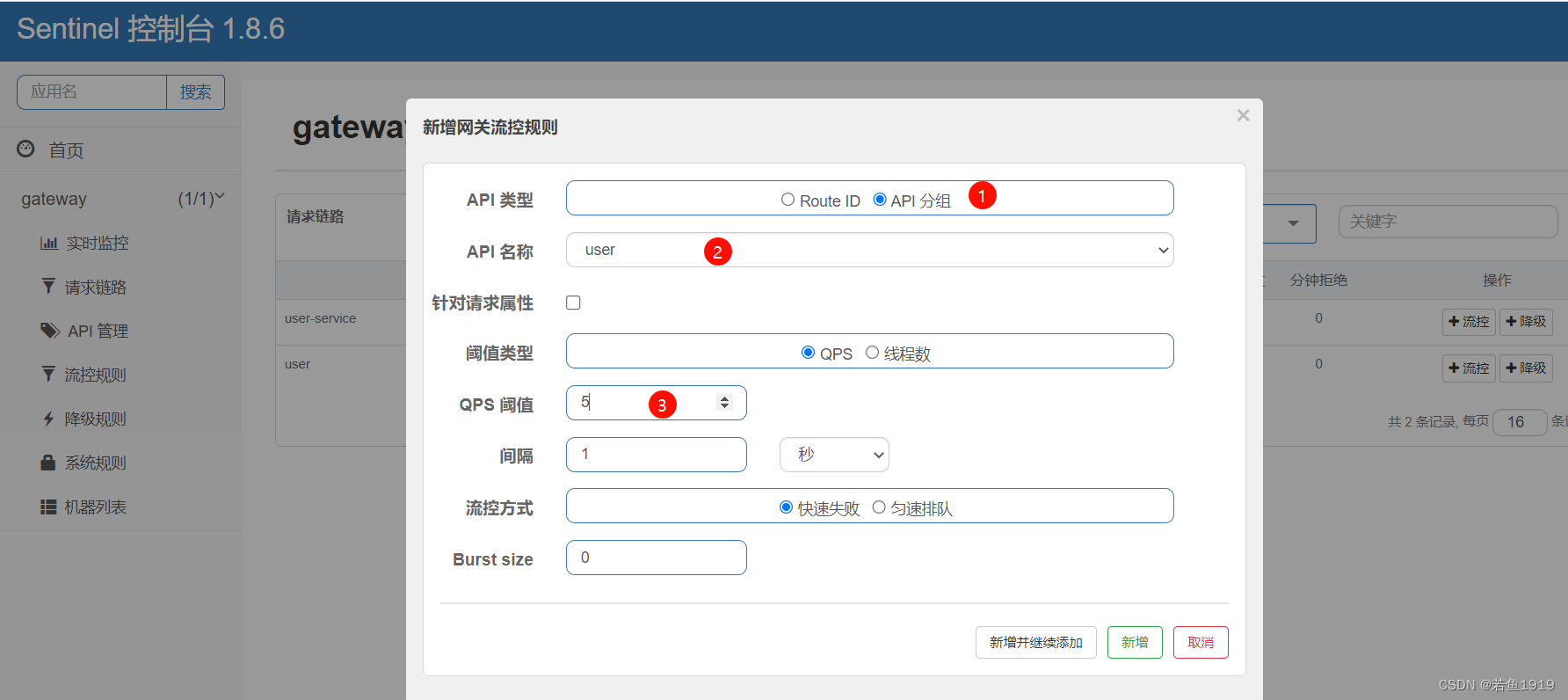
Spring-Cloud-Gateway集成Sentinel限流
1)gateway添加sentinel相关依赖
<spring-cloud.version>2021.0.1</spring-cloud.version>
<spring-cloud-alibaba.version>2021.0.1.0</spring-cloud-alibaba.version><dependencies><!--gateway--><dependency><gro…
C#,数值计算,求解微分方程的吉尔(Gear)四阶方法与源代码
1 微分方程
微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。 微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛,可以解决许多与导数…
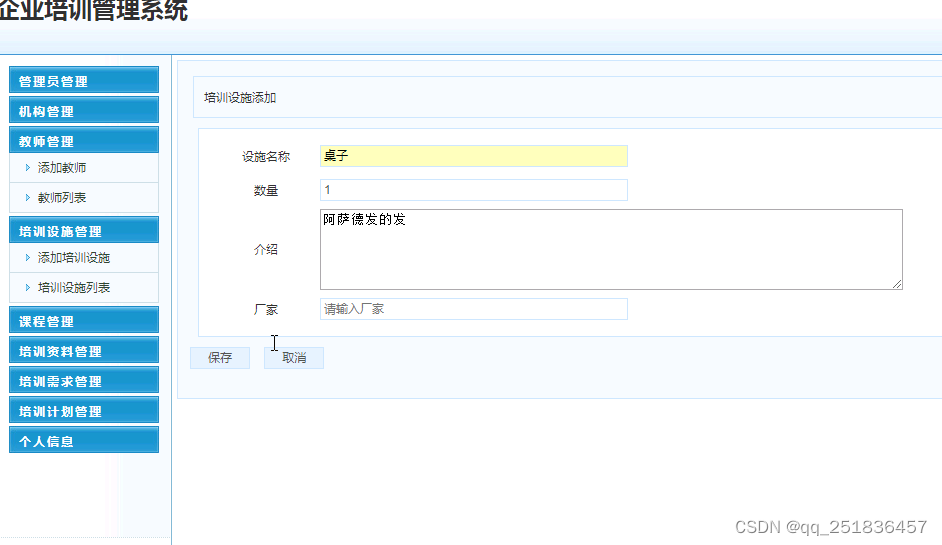
java 企业培训管理系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 java 企业培训管理系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发,数据库为Mysql5.0&…
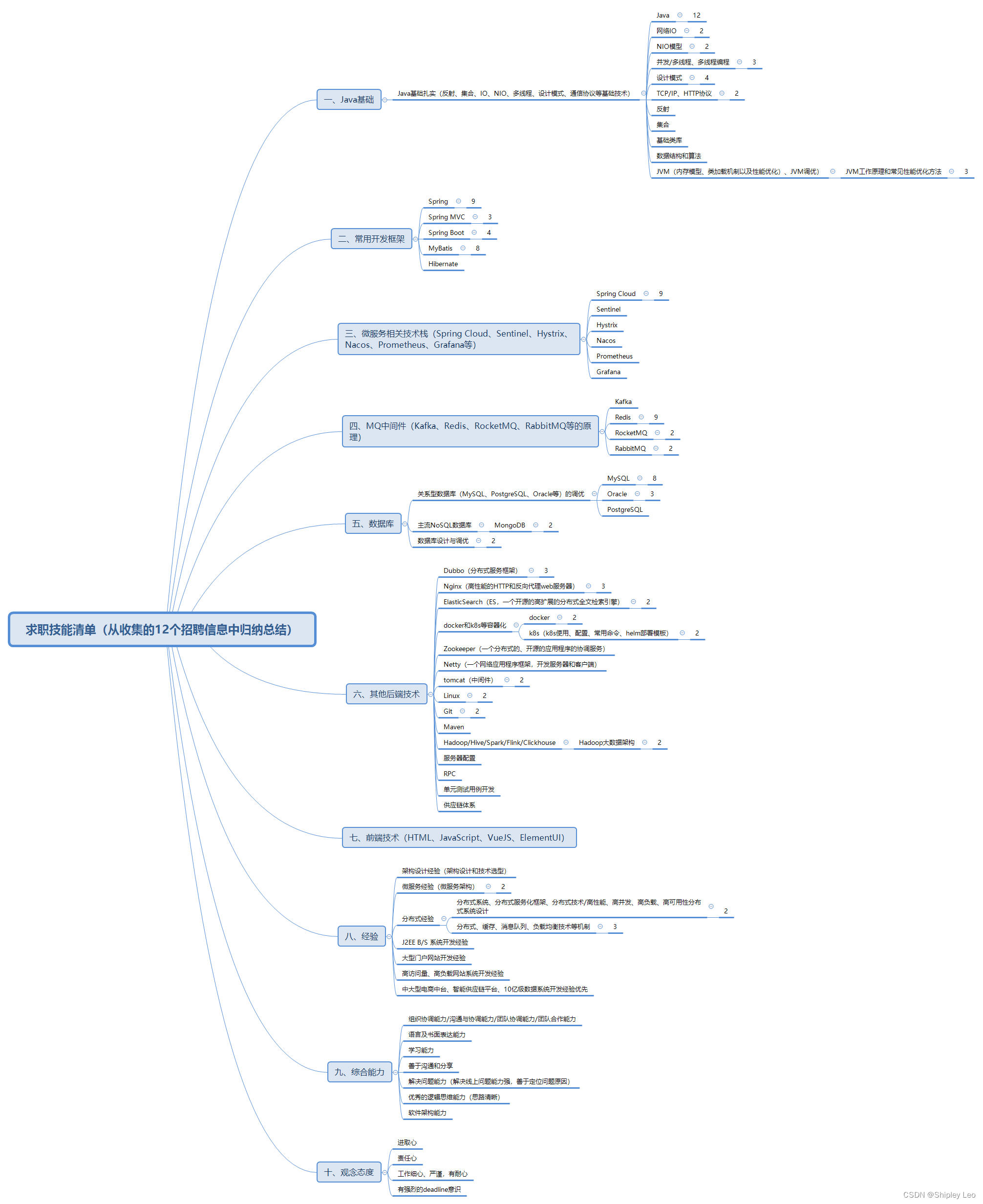
Java求职技能清单(2024版)
一、Java基础扎实(反射、集合、IO、NIO、多线程、设计模式、通信协议等基础技术) (一)Java (二)网络IO (三)NIO模型 (…
鸿蒙Harmony应用开发—ArkTS声明式开发(自定义事件分发)
ArkUI在处理触屏事件时,会在触屏事件触发前进行按压点和组件区域的触摸测试,来收集需要响应触屏事件的组件,再基于触摸测试结果分发相应的触屏事件。在父节点,开发者可以通过onChildTouchTest决定如何让子节点去做触摸测试&#x…
MFC web文件 CHttpFile的使用初探
MFC CHttpFile的使用
两种方式,第一种OpenURL,第二种SendRequest,以前捣鼓过,今天再次整结果发现各种踩坑,好记性不如烂笔头,记录下来。
OpenURL
这种方式简单粗暴,用着舒服。
try
{//OpenU…