本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/377140.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
【CSP试题回顾】201703-1-分蛋糕
CSP-201703-1-分蛋糕
解题代码
#include <iostream>
using namespace std;int n, k, a, sumWeight, num;int main() {cin >> n >> k;for (int i 0; i < n; i){cin >> a;sumWeight a;if (sumWeight > k){num;sumWeight 0;}else if (i (n -…
【AI+CAD】(二)LLM和VLM生成结构化数据结构(PPT/CAD/DXF)
当前LLM和VLM在PPT生成任务上已经小有成效,如ChatPPT。 @TOC
1. PPT-LLM
LLM根据用户的instruction生成规范的绘制ppt的API语句:即使是最强的GPT-4 + CoT也只能达到20-30%的内容准确度。 LLM输入:User_instruction(当前+过去)、PPT_content、PPT_reader_API。其中 PPT_rea…
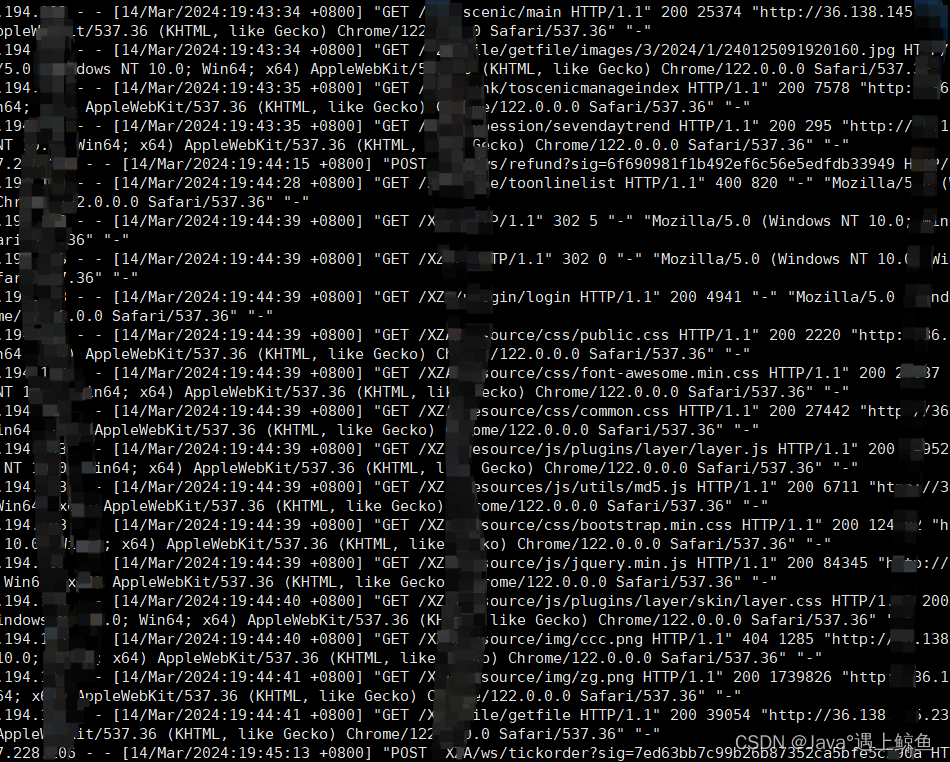
Nginx的日志怎么看,在哪看,access.log日志内容详解
Nginx 的日志文件通常位于服务器的文件系统中,具体位置可能因配置而异。以下是查看 Nginx 日志的几种方法:
1、查看访问日志:在默认配置下,Nginx 的访问日志文件路径为 /var/log/nginx/access.log。您可以通过命令 sudo cat /var…
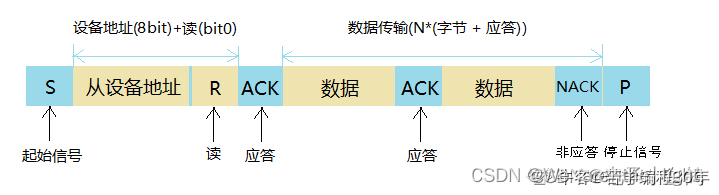
串行通信——UART总结
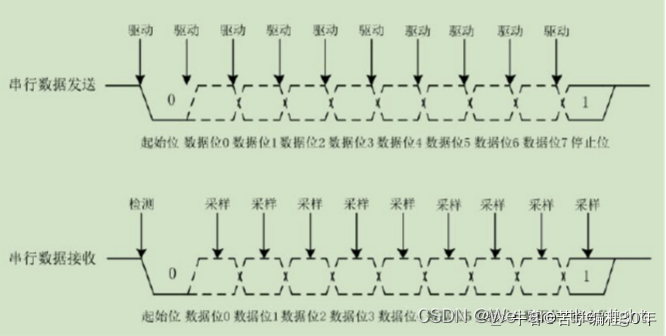
1. 什么是UART通信协议?
UART是异步,全双工串口总线。它比同步串口复杂很多。有两根线,一根TXD用于发送,一根RXD用于接收。UART的串行数据传输不需要使用时钟信号来同步传输,而是依赖于发送设备和接收设备之间预定义的…
【SSM】任务列表案例 基本CRUD SSM整合
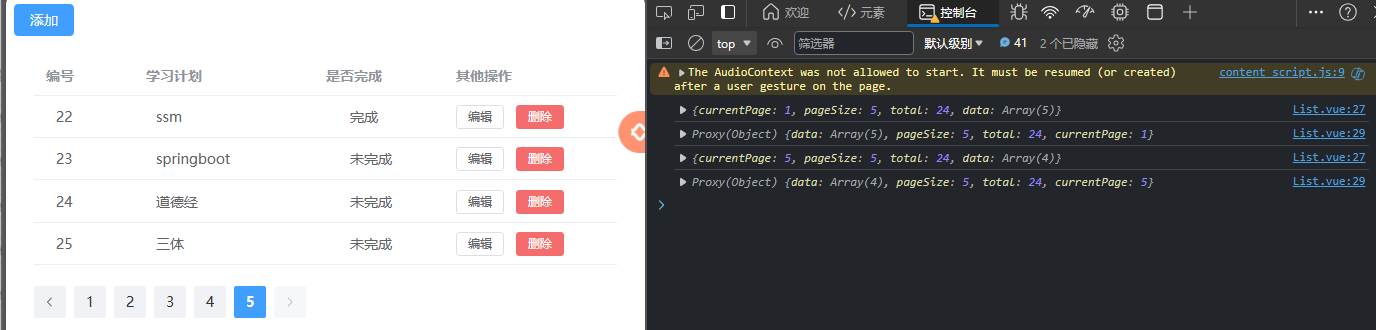
文章目录 一、案例功能预览二、接口分析三、前端工程导入四、后端程序实现和测试4.1 准备4.2 功能实现4.2.1 分页查询显示4.2.2 添加计划4.2.2 删除计划4.2.3 修改计划 4.3 前后联调 一、案例功能预览
Github 地址 : ssm-integration-part
二、接口分析
学习计划…
vue生命周期函数原理解析,vue阻止事件冒泡方法实现
✨✨ 欢迎大家来到景天科技苑✨✨
🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…
串行通信——IIC总结
一.什么是IIC?
IIC(Inter-Integrated Circuit)也称I2C,中文叫集成电路总线。是一个多主从的串行总线,由飞利浦公司发明的通讯总线,属于半双工同步传输类总线,仅由两条线就能完成多机通讯&#…
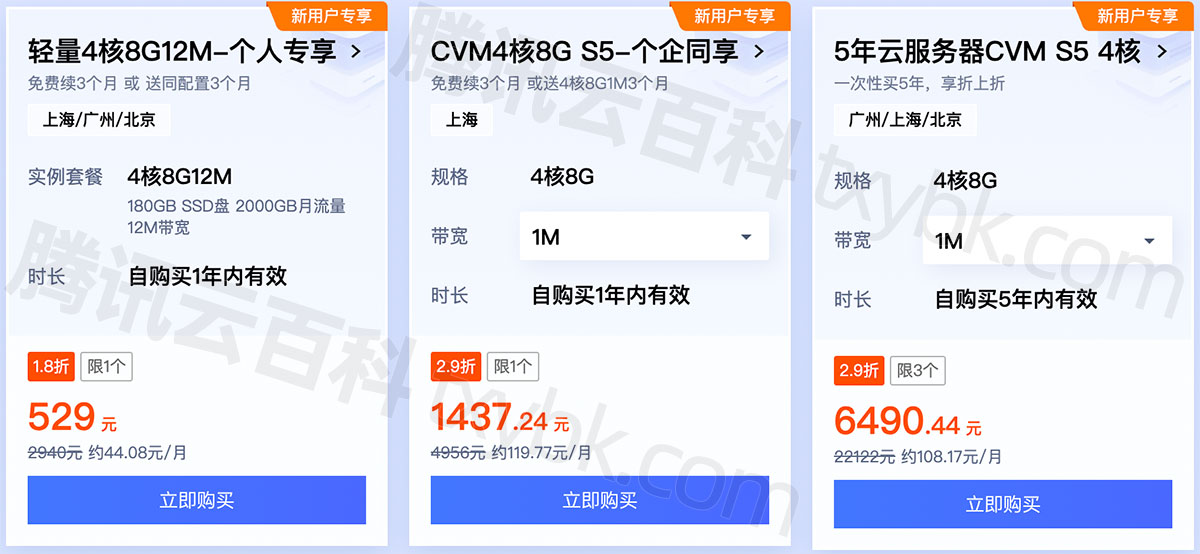
腾讯云和阿里云4核8G云服务器多少钱一年和1个月费用对比
4核8G云服务器多少钱一年?阿里云ECS服务器u1价格955.58元一年,腾讯云轻量4核8G12M带宽价格是646元15个月,阿腾云atengyun.com整理4核8G云服务器价格表,包括一年费用和1个月收费明细:
云服务器4核8G配置收费价格
阿里…
场的概念---数量场(标量场)和矢量场介绍理解
目录 一、场的概念
二、场的分类
三、数量场(标量场)的等值面
四、矢量场中的矢量线
矢量线方程推导: 一、场的概念
场在数学上是指一个向量到另一个向量或数的映射。场指物体在空间中的分布情况。场是用空间位置函数来表征的。在物理学…
nvm安装,nvm使用及常用命令,node版本管理
安装包下载地址
下载使用
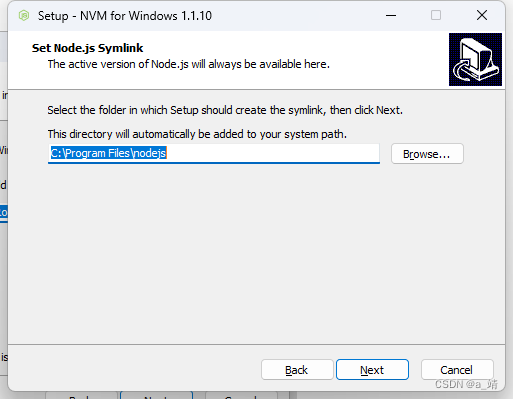
安装:
点击 nvm-setup.exe,按下图步骤安装, 下一步 安装完成后使用:
打开命令行输入下面的常用命令就可以自由管理node版本了,更换node版本,npm会自动更新到对应node匹配的版本…
ARM/Linux嵌入式面经(六):华为【共四面】
面试一共四面,面试岗位为嵌入式工程师。华为的面试官本次体验还是蛮好的,技术强,也比较温柔。下面开始进入正题吧~~~ 【一面】资格面
主要是问了有以下几点: 简历好奇我的专业,然后问我学过哪些学科。 项目当时抓我的项目,一个无线传感器网络的项目。没有问技术,主要问…
使用OpenCV实现两张图像融合在一起
简单介绍
图像融合技术是一种结合多个不同来源或不同传感器捕获的同一场景的图像数据,以生成一幅更全面、更高质量的单一图像的过程。这种技术广泛应用于遥感、医学影像分析、计算机视觉等多个领域。常见的图像融合技术包括基于像素级、特征级和决策级的融合方法&a…
使用nuclei扩充自己的武器库-nuclei3 sdk开发指南
一、nuclei是什么 Nuclei 是一个快速、灵活、可扩展的开源漏洞扫描工具,用于发现 Web 应用程序中的安全问题。它允许安全研究人员和渗透测试人员轻松地定义和执行定制的漏洞扫描任务。
Nuclei 使用模板来定义漏洞扫描任务。这些模板是基于 YAML 格式的,…
Visual Studio 2022 配置“Debug|x64”的 Designtime 生成失败。IntelliSense 可能不可用。
今天写代码,无缘无故就给我整个这个错误出来,我一头雾水。 经过我几个小时的奋战,终于解决问题 原因就是这个Q_INTERFACES()宏,我本想使用Q_DECLARE_INTERFACE Q_INTERFACES这两个Qt宏实现不继承QObject也能使用qobjec…
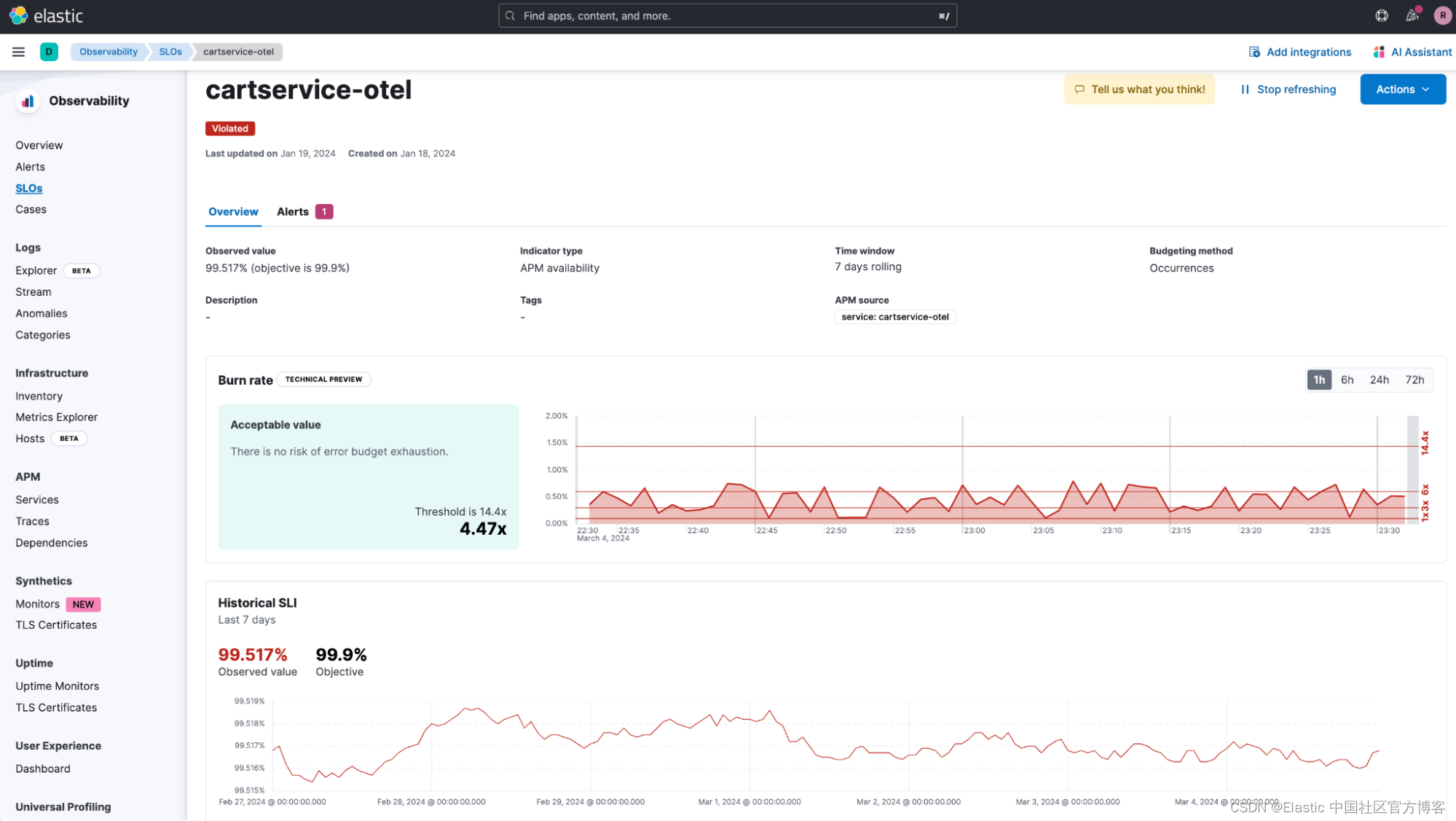
Observability:使用 Elastic AI Assistant 和 APM 分析 OpenTelemetry 应用程序
作者:来自 Elastic Bahubali Shetti OpenTelemetry 正在迅速成为云原生计算基金会 (CNCF) 内最广泛的项目,拥有与 Kubernetes 一样多的提交,并获得了客户的广泛支持。 许多公司正在采用 OpenTelemetry 并将其集成到他们的应用程序中。 Elasti…
springboot项目自定义切面增强方法功能(springboot记录日志)
说明
背景:记录系统接口日志入库,包含接口方法、入参、回参、响应时间、操作人、操作时间等信息。
方案:添加自定义切面处理
一、自定义切面注解
package com.gstanzer.supervise.annotation;import com.gstanzer.supervise.enums.Busine…
国创证券策略:股指预计维持震荡格局 关注汽车、通信设备等板块
国创证券指出,近期两市指数持续反弹创新高,但沪指现已率先出现滞涨状况,一起均已进入阻力重压区。不过当时技术形状上坚持较好,可持续做多,一旦跌破重要支撑如沪指的3030点,则需降仓防卫,防止指…
C#,数值计算,数据测试用的对称正定矩阵(Symmetric Positive Definite Matrix)的随机生成算法与源代码
C.Hermite
1、对称矩阵
对称矩阵(Symmetric Matrices)是指以主对角线为对称轴,各元素对应相等的矩阵。在线性代数中,对称矩阵是一个方形矩阵,其转置矩阵和自身相等。1855年,埃米特(C.Hermite,1822-1901年)证明了别的数学家发现的一些矩阵类的特征根的特殊性质,如称为埃…