本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/421742.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
嵌入式学习——C语言基础——day11
1. 字符型数组和字符串的传参 1.1 常量和变量的区别(难点) 一般常量不能被修改,变量才能被修改
#include <stdio.h>
int main(void) { char str[] {"hello world"};//定义数组,数组名为指针常量 char …
提示词优化的自动化探索:Automated Prompt Engineering
编者按: 作者在尝试教授母亲使用 LLM 完成工作任务时,意识到提示词的优化并不像想象中简单。提示词的自动优化对于经验并不丰富的提示词撰写者很有价值,他们没有足够的经验去调整和改进提供给模型的提示词,这引发了对自动化提示词…
Linux——web基础实验
实验前的安装
[rootwebserver ~]# yum -y install httpd
[rootwebserver ~]# systemctl enable --now httpd
Created symlink /etc/systemd/system/multi-user.target.wants/httpd.service →
/usr/lib/systemd/system/httpd.service.
[rootwebserver ~]# echo test for apach…
在React Router 6中使用useRouteLoaderData钩子获取自定义路由信息
在 React Router 6 中怎么像vueRouter一样,可以在配置路由的时候,定义路由的元信息(附加信息)?答案是可以的。稍有些复杂。核心是通过为每个路由定义了一个 loader 函数,用于返回自定义的路由信息,然后通过useRouteLoaderData 钩子…
C#基础|StringBuilder字符串如何高效处理。
哈喽,你好,我是雷工。 字符串处理在C#程序开发中是使用频率比较高的,但常规的字符串处理方式对内存占用比较多,为了优化内存,减少不必要的内存浪费,引入了StringBuilder类。 下面学习下StringBuilder类的使…
SEGGER Embedded Studio IDE移植FreeRTOS
SEGGER Embedded Studio IDE移植FreeRTOS 一、简介二、技术路线2.1 获取FreeRTOS源码2.2 将必要的文件复制到工程中2.2.1 移植C文件2.2.2 移植portable文件2.2.3 移植头文件 2.3 创建FreeRTOSConfig.h并进行配置2.3.1 处理中断优先级2.3.2 configASSERT( x )的处理2.3.3 关于系…
【win10相关】更新后出现未连接到互联网的问题及解决
问题背景
在win10更新完系统之后,第二天电脑开机后,发现无法上网,尝试打开百度,但是出现以下图片: 经过检查,发现手机是可以上网的,说明网络本身并没有问题,对防火墙进行了一些设置…
使用Umbrello学习工厂模式
工厂方法模式之所以有一个别名叫多态性工厂模式是因为具体工厂类都有共同的接口, 或者有共同的抽象父类。 当系统扩展需要添加新的产品对象时,仅仅需要添加一个具体对象以及一个具体工厂对 象,原有工厂对象不需要进行任何修改,也不…
Python快速入门1数据类型(需要具有编程基础)
数据类型:
Python 3.0版本中常见的数据类型有六种:
不可变数据类型可变数据类型Number(数字)List(列表)String(字符串)Dictionary(字典)Tuple(元…
进程控制5 - exit()退出+子进程被收养+僵死进程
我们应当知道的是,在用fork创建子进程后,父子进程的执行的先后顺序是不定的,这时,我们可以用wait函数,wait()会暂停当前进程的执行,直到有信号到来或者子进程结束。总的来说,wait()的作用就是阻…
AutoGPT-Forge使用教程,自行构建agent智能体
本博客给出AutoGPT-forge四个教程的翻译与理解,使用GPT4翻译,
参考官方教程https://aiedge.medium.com/autogpt-forge-a-comprehensive-guide-to-your-first-steps-a1dfdf46e3b4
使用AutoGPT Github代码日期2024/4/22;
博客开始编辑日期20…
Qt | 窗口的显示及可见性|标题、透明度、启用/禁用|窗口标志、设置其他属性|获取窗口部件、设置父部件|鼠标光标
显示事件:QEvent::show,处理函数为 showEvent(QShowEvent*)
隐藏事件:QEvent::hide,处理函数为 hideEvent(QHideEvent* )
01 QWidget 类中与可见性有关的属性
visible:bool
访问函数:
bool isVisible() const;
virtual void setVisible(bool visible);
02 QWid…
面试八股——HashMap
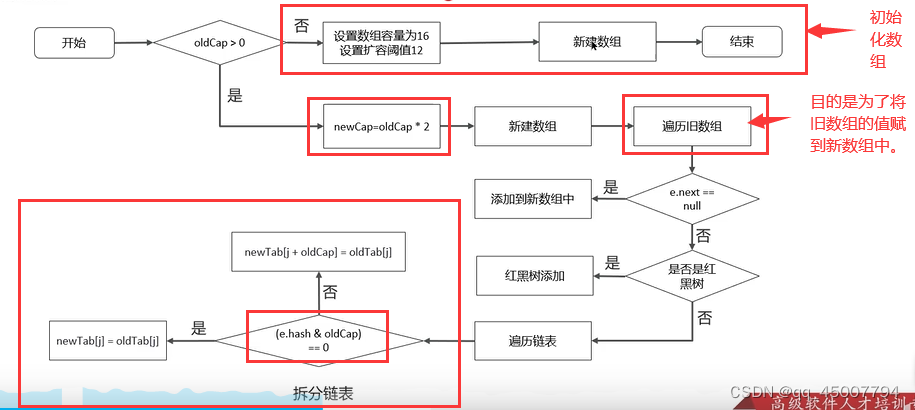
实现原理 红黑树是为了解决链表过长之后,查找时间过长的问题,将链表存储变为红黑树存储。
put方法的实现(5⭐)
相关属性:
1. 容量:初始容量为2^4。 2. 加载因子:初始值为0.75 上面两个属性的…
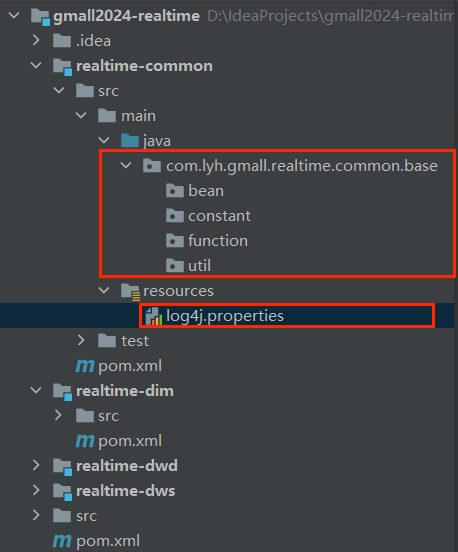
Flink 实时数仓(一)【实时数仓离线数仓对比】
前言 昨天技术面的时候,面试官说人家公司现在用的都是最新的技术,比如 Doris 等一些最新的工具,确实这些课是学校永远不会开设的,好在他说去了会带着我做一做。可是 ...... 学院这边确实不允许放人,唉,可惜…
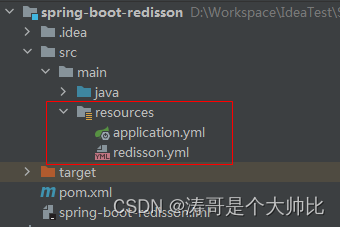
Spring Boot整合Redisson的两种方式
项目场景
Spring Boot整合Redisson的两种方式,方式一直接使用yml配置,方式二创建RedissonConfig配置类。 前言 redisson和redis区别: Redis是一个开源的内存数据库,支持多种数据类型,如字符串、哈希、列表、集合和有序…
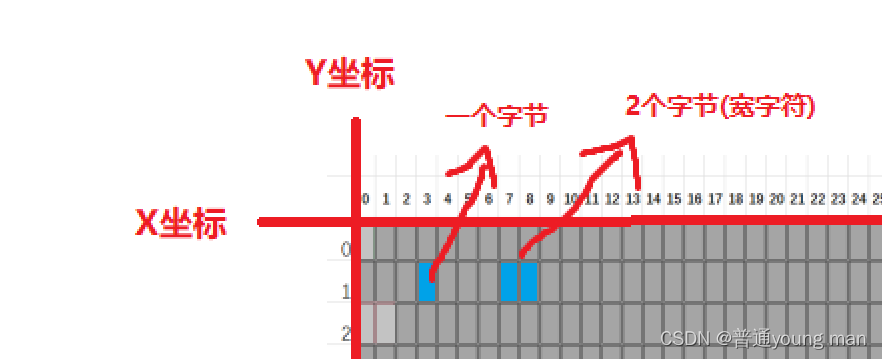
宽字符的来历:从ASCII到Unicode,C语言中的宽字符处理
目录
一、ASCII编码:字符世界的开篇
二、Unicode与宽字符的诞生
宽字符类型与宽字符串
三、C语言中的宽字符处理函数
四、宽字符与多字节字符
结语 在计算机科学的发展历程中,字符编码经历了从简单到复杂、从单一语言到全球多语种支持的演变过程。…
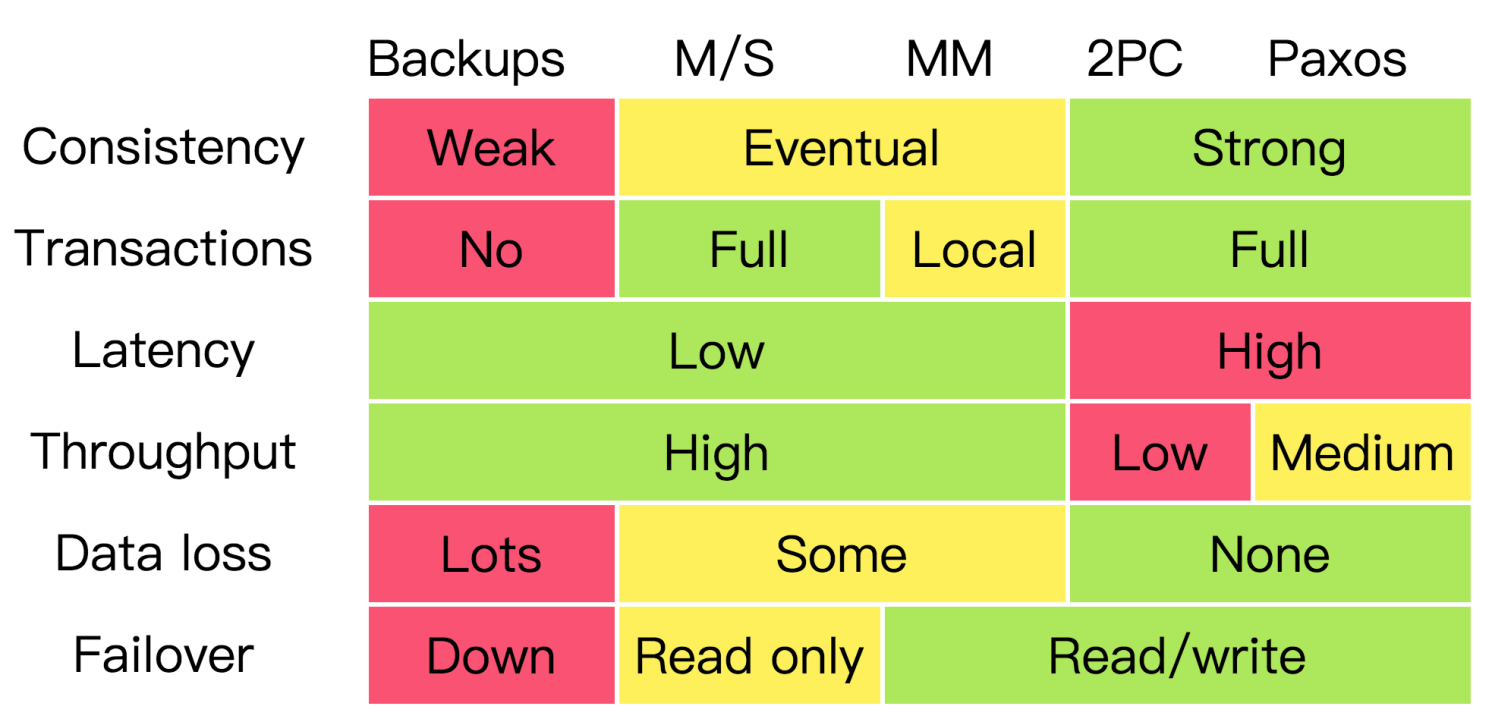
从Kafka的可靠性设计体验软件设计之美
目录 1. Kafka可靠性概述
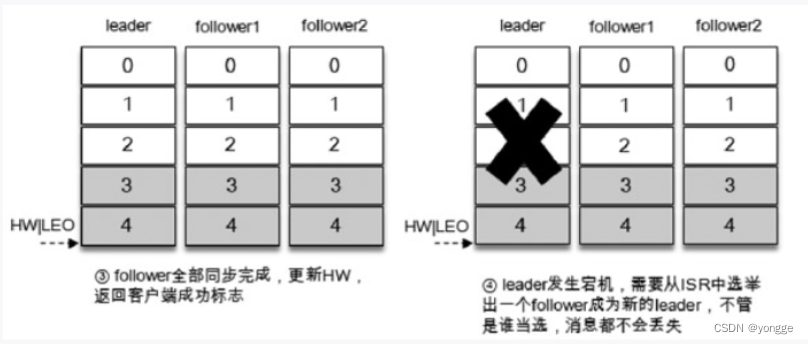
2. 副本剖析 2.1 什么是副本 2.2 副本失效场景 2.3 数据丢失场景
2.4 解决数据丢失方案
3. 日志同步机制
4. 可靠性分析 1. Kafka可靠性概述 Kafka 中采用了多副本的机制,这是大多数分布式系统中惯用的手法,以此来实现水平扩…
Git 常用命令大全
🚀 Git安装与基础知识学习 🌐 🎯 Git作为一款全球开发者广泛使用的分布式版本控制系统,能够有效帮助团队协作并追踪项目历史版本。接下来,我们将详细展开Git的安装流程、基础命令操作、高级用法以及应对常见问题的方法…
模块四:前缀和——DP35 【模板】二维前缀和
文章目录 题目描述算法原理解法一:暴力模拟(时间复杂度为O(n*m*q))解法二:二维前缀和(时间复杂度为O(m*n)O(q)) 代码实现解法二:前缀和(C)Java 题目描述
题目链接:DP35 【模板】二维…