本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/4446.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
短视频矩阵营销系统技术开发者开发笔记分享
一、开发短视频seo抖音矩阵系统需要遵循以下步骤:
1. 确定系统需求:根据客户的需求,确定系统的功能和特点,例如用户注册登录、视频上传、视频浏览、评论点赞等。
2. 设计系统架构:根据系统需求,设计系统的…
PostMan+Jmeter+QTP工具介绍及安装
目录
一、PostMan介绍编辑
二、下载安装
三、Postman与Jmeter的区别
一、开发语言区别:
二、使用范围区别:
三、使用区别:
四、Jmeter安装
附一个详细的Jmeter按照新手使用教程,感谢作者,亲测有效。 五、Jme…
在排序数组中查找元素的第一个和最后一个位置——力扣34
文章目录 题目描述法一 二分查找 题目描述 法一 二分查找 int bsearch_1(int l, int r)
{while (l < r){int mid (l r)/2;if (check(mid)) r mid;else l mid 1;}return l;
}int bsearch_2(int l, int r)
{while (l < r){int mid ( l r 1 ) /2;if (check(mid)) l …
牛客网Verilog刷题——VL55
牛客网Verilog刷题——VL55 题目答案 题目 请用Verilog实现4位约翰逊计数器(扭环形计数器),计数器的循环状态如下: 电路的接口如下图所示: 输入输出描述:
信号类型输入/输出位宽描述clkwireInput1系统…
HarmonyOS 开发基础(二)组件拼凑简单登录页面
一、简单登录页面 Entry
Component
/*
组件可以基于struct实现,组件不能有继承关系,struct可以比class更加快速的创建和销毁。*/
struct Index {State message: string Hello Worldbuild() {// https://developer.harmonyos.com/cn/docs/documentation/…
【微软知识】微软相关技术知识分享
微软技术领域
一、微软操作系统:
微软的操作系统主要是 Windows 系列,包括 Windows 10、Windows Server 等。了解 Windows 操作系统的基本使用、配置和故障排除是非常重要的。微软操作系统(Microsoft System)是美国微软开发的Wi…
@monaco-editor/react组件CDN加载失败解决办法
monaco-editor/react引入这个cdn资源会load失败 网上很多例子都是这样写的,我这样写monaco会报错
import * as monaco from monaco-editor;
import { loader } from monaco-editor/react;loader.config({ monaco });改成这样
import * as monaco from monaco-edi…
P3372 【模板】线段树 1(内附封面)
【模板】线段树 1
题目描述
如题,已知一个数列,你需要进行下面两种操作:
将某区间每一个数加上 k k k。求出某区间每一个数的和。
输入格式
第一行包含两个整数 n , m n, m n,m,分别表示该数列数字的个数和操作的总个数。 …
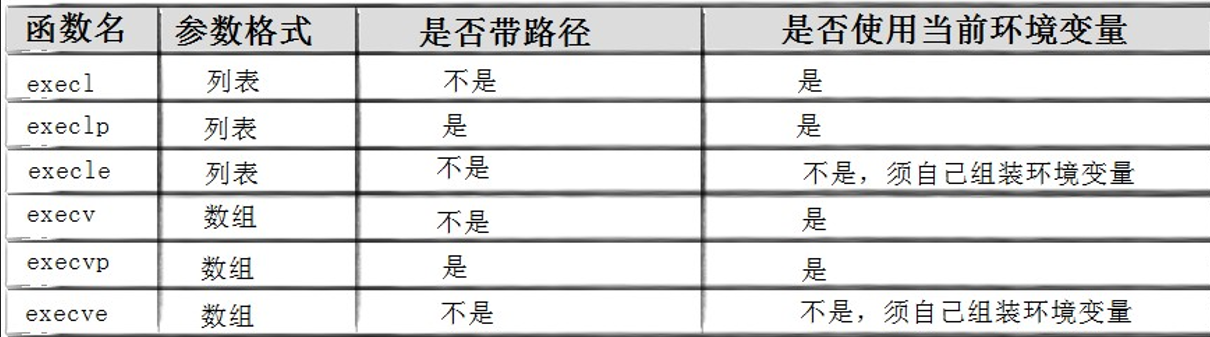
Linux - 进程控制(进程替换)
0.引入 创建子进程的目的是什么? 就是为了让子进程帮我执行特定的任务 让子进程执行父进程的一部分代码 如果子进程想执行一个全新的程序代码呢? 那么就要使用 进程的程序替换 为什么要有程序替换? 也就是说子进程想执行一个全新的程序代码&a…
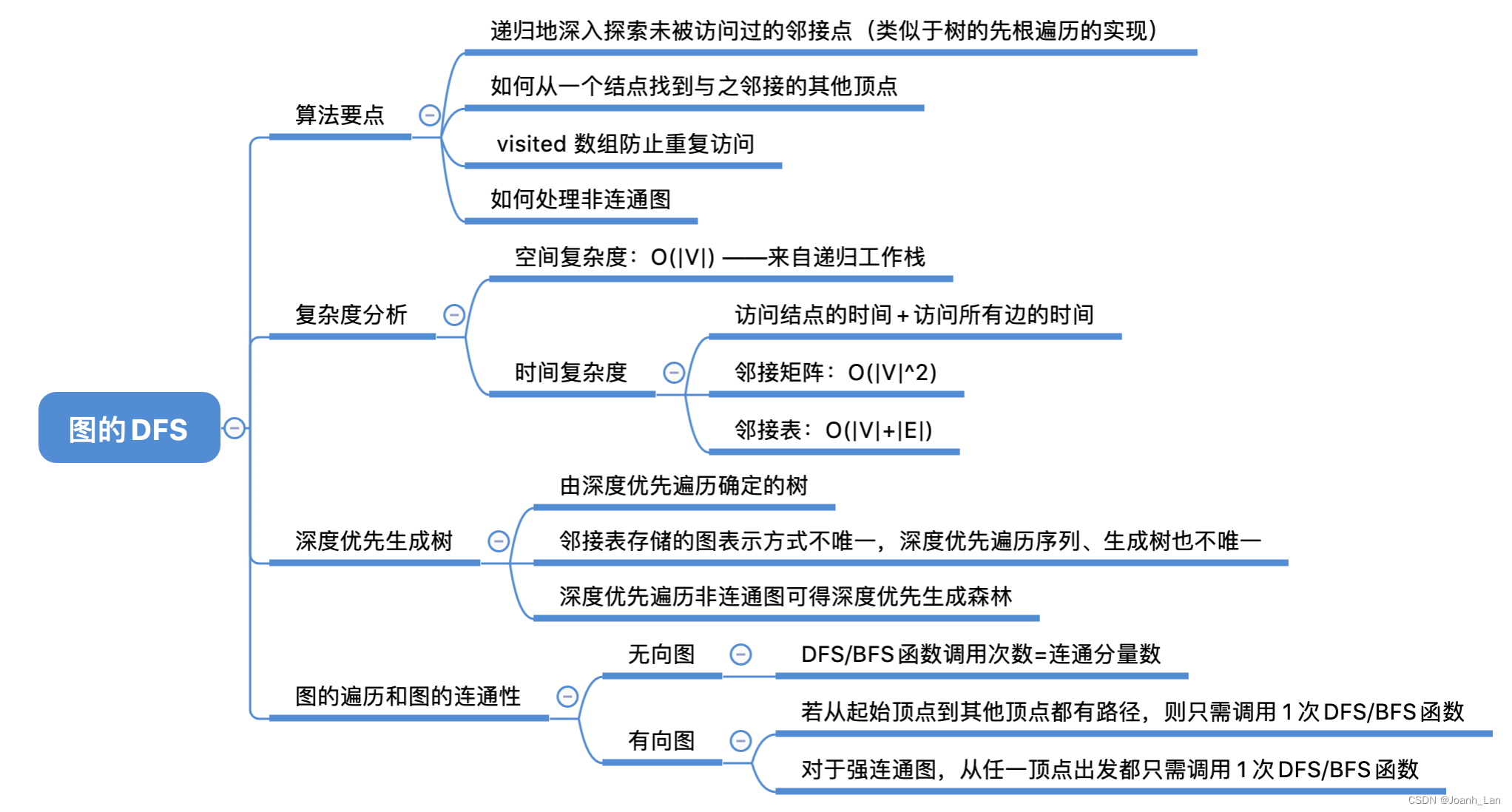
数据结构--图的遍历 DFS
数据结构–图的遍历 DFS 树的深度优先遍历 //树的先根遍历
void PreOrder(TreeNode *R)
{if(R ! NULL){visit(R); //访问根节点while(R还有下一个子树T)PreOrder(T);//先根遍历下一棵子树}
}图的深度优先遍历 bool visited [MAX_VERTEX_NUM]; //访问标记数组
void DFS(Grap…
【MyBatis】 框架原理
目录
10.3【MyBatis】 框架原理
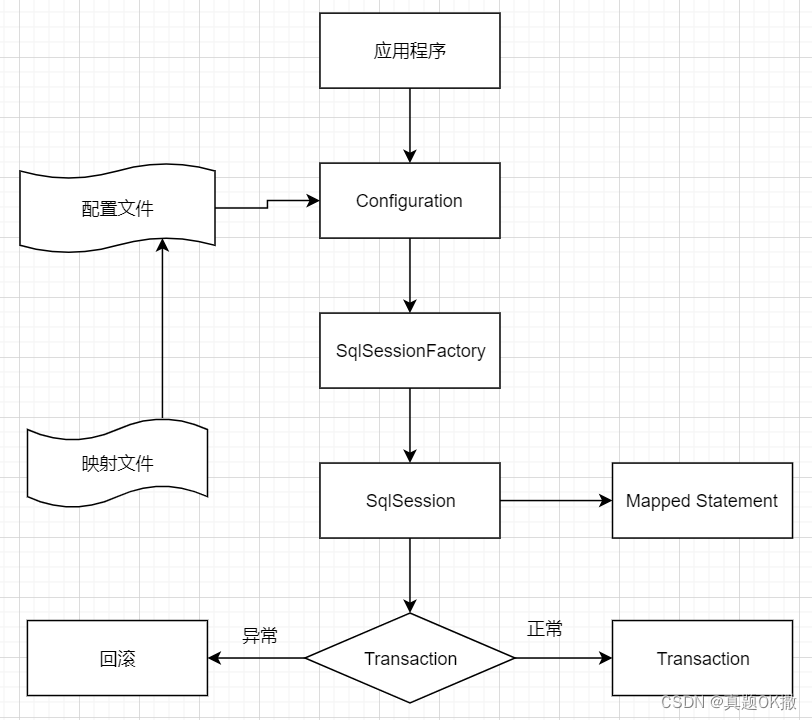
10.3.1 【MyBatis】 整体架构
10.3.2 【MyBatis】 运行原理
10.4 【MyBatis】 核心组件的生命周期
10.4.1 SqlSessionFactoryBuilder
10.4.2 SqlSessionFactory
10.4.3 SqlSession
10.4.4 Mapper Instances 与 Hibernate 框架相比&#…
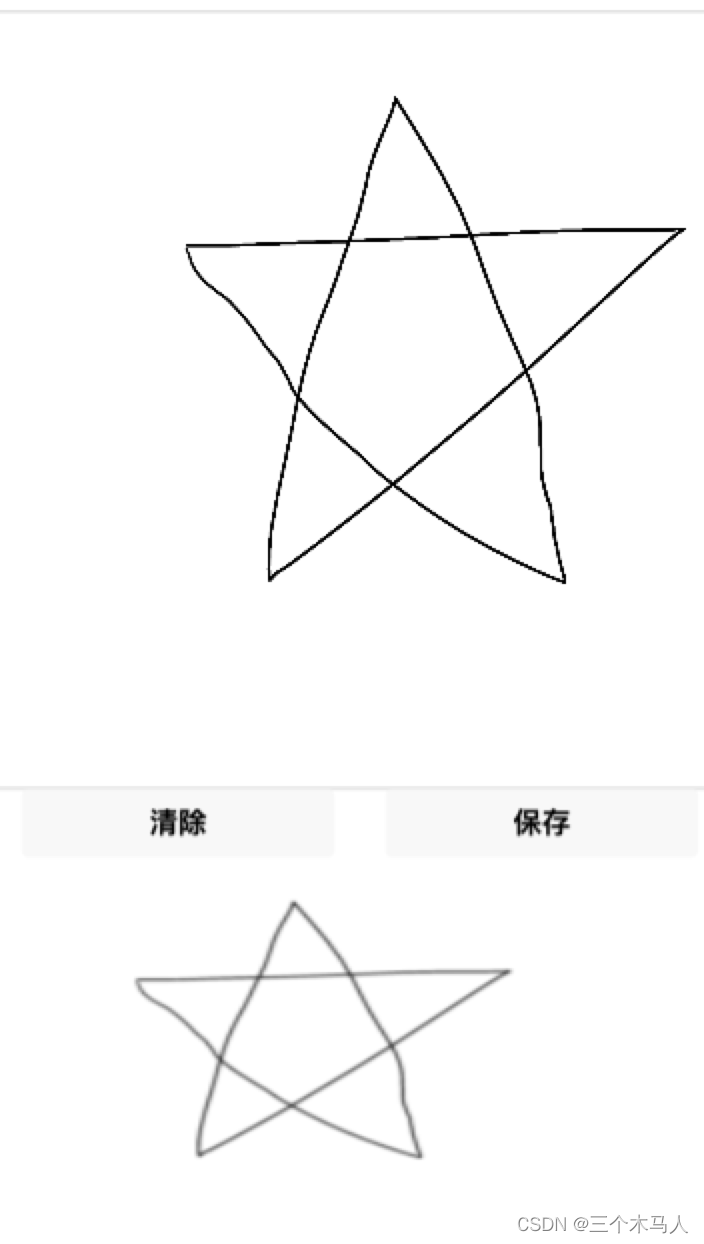
微信小程序使用 canvas 2d 实现签字板组件
本文是在微信小程序中使用 canvas 2d 来实现签字板功能;
效果图: 代码: 1、wxml
<view><canvas id"canvas"type"2d"bindtouchstart"start"bindtouchmove"move"bindtouchend"end&qu…
session反序列化+SoapClientSSRF+CRLF
文章目录 session反序列化SoapClientSSRFCRLF前言bestphps revengecall_user_func()方法的特性SSRFCRLF组合拳session反序列化 解题步骤总结 session反序列化SoapClientSSRFCRLF
前言
从一道题分析通过session反序列化出发SoapClientSSRF利用CRLF解题
bestphp’s revenge
首…
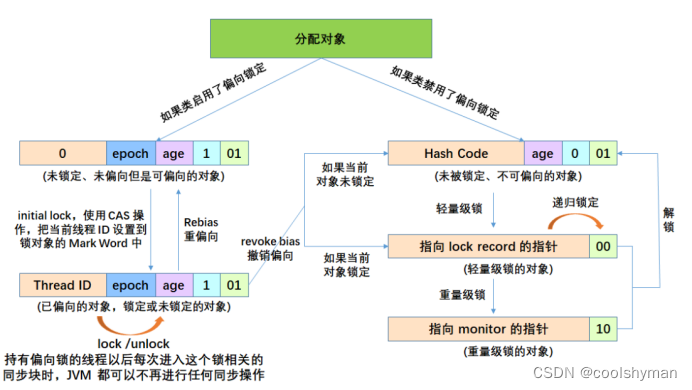
Java并发系列之二:悲观锁机制
什么是锁
在并发环境下,会出现多个线程对同一个资源进行争抢的情况,假设A线程对资源正在进行修改,此时B线程此时又对资源进行了修改,这就可能会导致数据不一致的问题。为了解决这个问题,很多编程语言引入了锁机制&…
2023.7月最新ORACLE考试通过|微思-ORACLE官方授权中心
微思-ORACLE官方授权培训中心 2022 ORACLE OCP考试战报https://blog.csdn.net/XMWS_IT/article/details/125866726?ops_request_misc%257B%2522request%255Fid%2522%253A%2522169089281916800182194373%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&r…
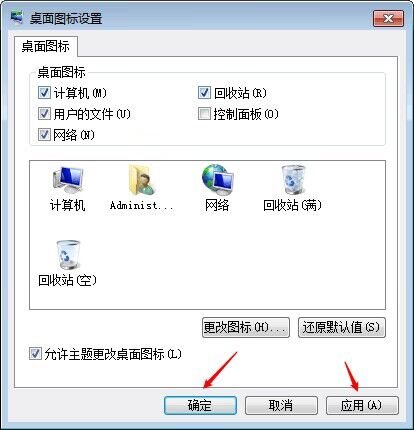
电脑如何显示回收站图标及回收站数据恢复教程
案例:“电脑如何显示回收站图标?我不记得自己做了什么。电脑桌面上没有回收站图标了,现在我迫切需要还原回收站里面的文件,我希望您能帮帮我,给我提供一些解决这个问题的方法。非常感谢!”
回收站通常以一…
电脑主机启动不起来怎么回事?2023最新解决方法!
“我的电脑刚用才没多久,怎么主机突然就启动不起来了呢?试了很多方法还是不行,这我该怎么解决呀?”
在日常的学习和工作中,大多数人已经离不开电脑了。当然,在使用电脑的过程中,会遇到各种各样…
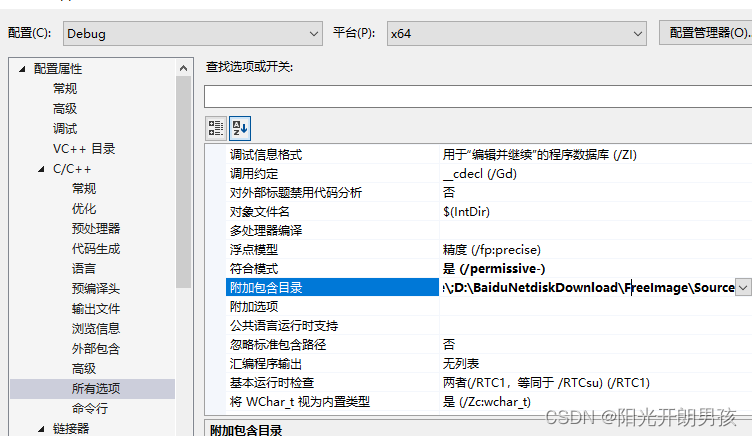
Windows下FreeImage库的配置
首先下载FreeImage库,http://freeimage.sourceforge.net/download.html,官网下载如下: 内部下载地址:https://download.csdn.net/download/qq_36314864/88140305
解压后,打开FreeImage.2017.sln,如果是vs…
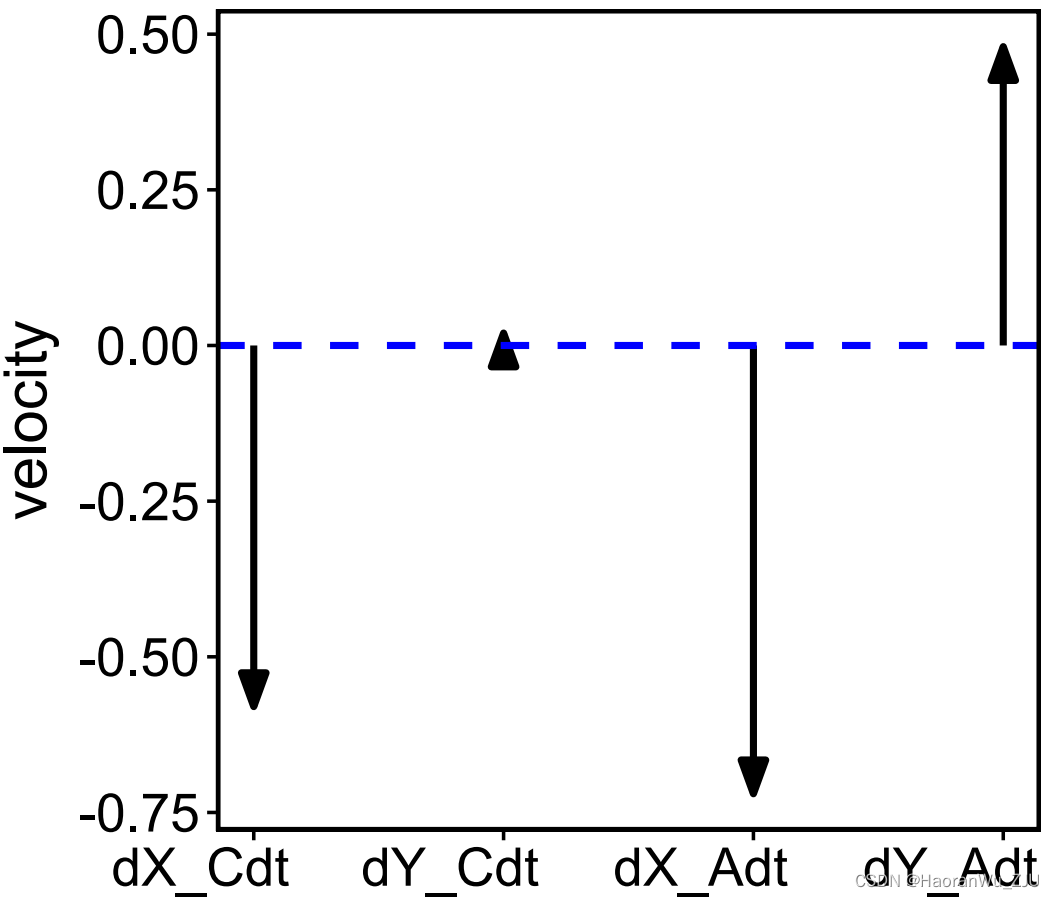
常微分方程建模R包ecode(二)——绘制相速矢量场
本节中我们考虑一个更为复杂的常微分方程模型, d X C d t ν ( X A Y A ) − β ⋅ X C ⋅ ( Y C Y A ) − ( μ g ) ⋅ X C , ( 1 ) d Y C d t β ⋅ X C ⋅ ( Y C Y A ) − ( μ g ρ ) ⋅ Y C , ( 2 ) d X A d t g ⋅ X C − β ⋅ X A ⋅ ( Y C Y A …