本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/467205.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
单目深度估计模型 lite-mono 测试
lite-mono 使用工业数据集kitti 进行训练,目的使用单目摄像头实现物体深度预测,关于kitti数据集的介绍和下载参考
(二)一文带你了解KITTI数据集-CSDN博客文章浏览阅读2.7w次,点赞64次,收藏294次。文章介绍…
RK3588, FFmpeg 拉流 RTSP, mpp 硬解码转RGB
RK3588 ,基于FFmpeg, 拉取RTSP,使用 mpp 实现硬解码. ⚡️ 参考: Rk3588 FFmpeg 拉流 RTSP, mpp 硬解码转RGBUbuntu x64 架构, 交叉编译aarch64 FFmpeg mppCode RTSPint open_stream(
回归预测模型 | LSTM、CNN、Transformer、TCN、串行、并行模型集合
往期精彩内容:
时序预测:LSTM、ARIMA、Holt-Winters、SARIMA模型的分析与比较
全是干货 | 数据集、学习资料、建模资源分享!
EMD变体分解效果最好算法——CEEMDAN(五)-CSDN博客
拒绝信息泄露!VMD滚动分…
安装Ubuntu系统(操作记录)
一、安装双系统
在 Windows10 系统下安装 Ubuntu22.04 系统https://blog.csdn.net/weixin_44916154/article/details/124414659?spm1001.2014.3001.5506
Windows10下安装Ubuntu22.04(打造双系统)步骤 安装Nvidia显卡驱动https://blog.csdn.net/taked…
高效项目托管指南:从本地到 GitHub 的完整流程
在现代软件开发中,将项目托管在 GitHub 上是一个常见且高效的方式。GitHub 不仅可以用作版本控制工具,还能帮助你与团队协作或展示自己的项目。本文将带你一步步完成项目的打包和上传。 高效项目托管指南:从本地到 GitHub 的完整流程 1. 准备…
YOLOv8目标检测(四)_图片推理
YOLOv8目标检测(一)_检测流程梳理:YOLOv8目标检测(一)_检测流程梳理_yolo检测流程-CSDN博客
YOLOv8目标检测(二)_准备数据集:YOLOv8目标检测(二)_准备数据集_yolov8 数据集准备-CSDN博客
YOLOv8目标检测(三)_训练模型:YOLOv8目标检测(三)_训…
python 下载 b站视频 和音频
video_bvid:
import os
import requests
import json
import re
from bs4 import BeautifulSoup
import subprocess
# from detail_video import video_bvid# video_bvid 是一个从外部得到的单个视频ID
video_bvid BV1cx421Q7veclass BilibiliVideoAudio:def __in…
windows mysql5.7设置慢查询参数
如果没有my.ini,可以复制一份my-default.ini改个名字就可以。
注意重启mysql服务
mysql5.7 直接在配置文件my.ini 中写如下配置 log_slow_admin_statements ON log_slow_slave_statements ON slow_query_log 1 //开启慢查询 (很多博客说on off ,我本机my…
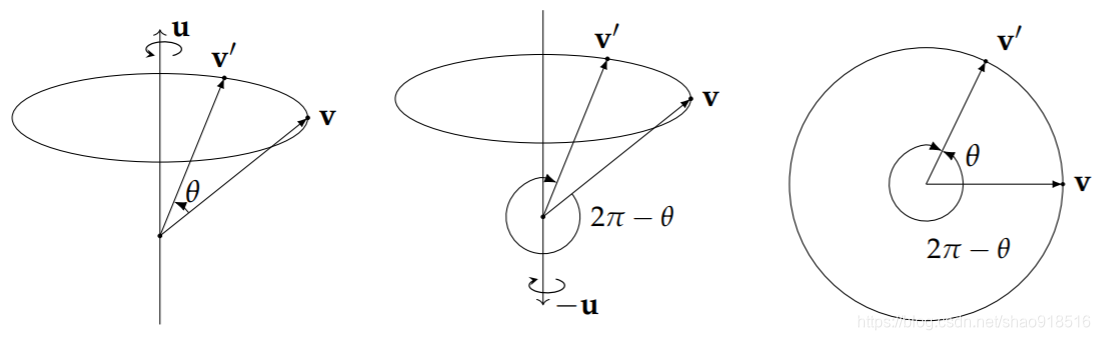
三维空间刚体运动4-1:四元数表示变换(各形式相互转换加代码——下篇)
三维空间刚体运动4-1:四元数表示变换(各形式相互转换加代码——下篇) 4. 四元数到其它旋转表示的相互转换4.1 旋转向量4.2 旋转矩阵4.3 欧拉角4.3.1 转换关系4.3.2 转换中的万象锁问题 5. 四元数的其他性质5.1 旋转的复合5.2 双倍覆盖5.3 指数…
嵌入式软考学习笔记(1)超详细!!!
目录
第一章计算机系统基础知识
1、逻辑运算
2、数的表示
3、总线系统
5、流水线
6、存储器
7、可靠性、校验码 第一章计算机系统基础知识
1、逻辑运算
与:有0则0,全1才1
或:有1则1,全0才0
异或:相同为0…
【数学】矩阵的逆与伪逆 EEGLAB
文章目录 前言matlab代码作用EEGLAB 中的代码总结参考文献 前言
在 EEGLAB 的使用中,运行程序时出现了矩阵接近奇异值,或者缩放错误。结果可能不准确。RCOND 1.873732e-20 的 bug,调查 EEGLAB 后发现是 raw 数据的问题。 matlab代码
A_1 …
快速理解类的加载过程
当程序主动使用某个类时,如果该类还未加载到内存中,则系统会通过如下三个步骤来对该类进行初始化: 1.加载:将class文件字节码内容加载到内存中,并将这些静态数据转换成方法区的运行时数据结构,然后生成一个…
HTTP 协议报文结构 | 返回状态码详解
注:本文为 “HTTP 历史 | 协议报文结构 | 返回状态码” 相关文章合辑。
未去重整理。 HTTP 历史
wangjunliang 最后更新: 2024/3/16 上午10:29
超文本传输协议(英语:HyperTextTransferProtocol,缩写:HTTP)是 万维网(World Wide Web)的基础协议。自 蒂姆…
VGGNet:深度学习中的卷积神经网络经典之作
目录
编辑
引言
VGGNet的历史背景
VGGNet的特点
1. 深度网络结构
2. 小卷积核的使用
3. 多尺度训练
4. 参数量的优化
5. 去除局部响应归一化
6. 优秀的特征提取能力
VGGNet的应用案例
VGGNet的代码复现
代码解析
结论 引言
在深度学习的浪潮中,卷积…
用 Python Turtle 绘制流动星空:编程中的璀璨星河
用 Python Turtle 绘制流动星空:编程中的璀璨星河 🐸 前言 🐸🐞往期绘画>>点击进所有绘画🐞🐋 效果图 🐋🐉 代码 🐉 🐸 前言 🐸 夜空中繁星…
【Tomcat】第五站:Servlet容器
Tomcat启动后,获取到项目当中所有的servlet的WebServlet中的配置信息。将配置信息和类对象都写入一个map集合当中。 map就是一个key-value类型的集合。
在MyTomcat中我们获取到了类对象和注解值。
Tomcat与请求连通
1. ServletConfigMapping 1. 创建一个config包…
[Java] 使用 VSCode 来开发 Java
目录 前言Java 环境怎么看自己是否已经配置完成?安装 JDK安装 Maven 环境修改 Maven 依赖源 完善 VS Code配置插件配置 Maven配置 Maven Settings配置 Maven 可执行文件地址 前言
由于使用 VSCode 编码已经成为习惯,并且它确实相对其他的 IDE 较为轻量化…
Linux学习——8_Linux下的火墙管理及优化
Linux下的火墙管理及优化
什么是防火墙
从功能角度来讲:防火墙是位于内部网和外部网之间的屏障,它按照系统管理员预先定义好的规则来控制数据包的进出 从功能实现角度来讲:火墙是系统内核上的一个模块netfilter(数据包过滤机制);…
联想至像M3070DW打印机连接手机方法
首先,按打印机上的“功能”键,上翻页翻到第4项“网络”按“OK”键进入; 点进去之后,再按下翻页翻到第3项“安装向导”,按“OK”键进入; 然后,选择我们要连接的WiFi并输入WiFi密码, 输…















![[Java] 使用 VSCode 来开发 Java](https://i-blog.csdnimg.cn/direct/45a6b5c90c9d469ea7c2bad3ef197bbc.png)

