本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/8432.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
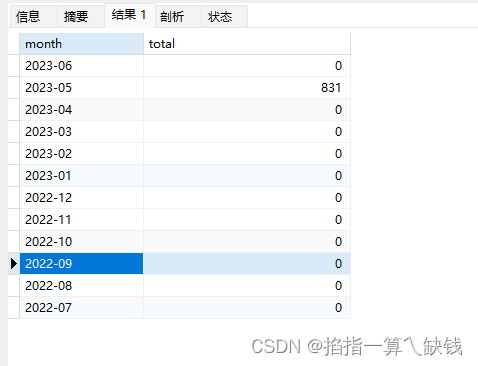
Mysql 查询统计最近12个月的数据
包括当月:
SELECTt1.yf AS month,count( t2.uuid ) AS total
FROM(SELECTDATE_FORMAT(( CURDATE()), %Y-%m ) AS yf UNIONSELECTDATE_FORMAT(( CURDATE() - INTERVAL 1 MONTH ), %Y-%m ) AS yf UNIONSELECTDATE_FORMAT(( CURDATE() - INTERVAL 2 MONTH ), %Y-%m ) AS yf UNION…
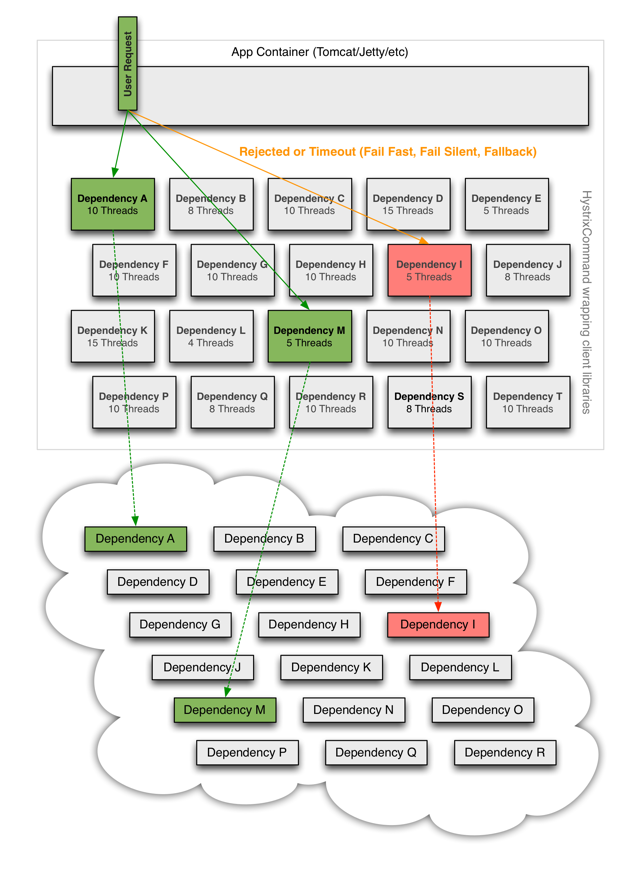
Spring Cloud
微服务架构 —》 新架构
模块化 功能化
用户 支付 签到 娱乐 …
人越来越多 一台服务器解决不了 在增加服务器 横向
假如 a 服务器 占用 98% 资源 b 服务器 只占用 10% 负载均衡
将原来的整体项目 分成模块化 用户就是一个单独的项目 签到也是一个单独的项目 项目和项目之…
Python——调用webdriver.Chrome() 报错
今天运行脚本,报错内容如下: collecting ... login_case.py:None (login_case.py) login_case.py:11: in <module> dr webdriver.Chrome() D:\Program Files (x86)\Python\Python39\Lib\site-packages\selenium\webdriver\chrome\webdriver.p…
多赛道出海案例,亚马逊云科技为企业提供全新解决方案实现高速增长
数字化浪潮之下,中国企业的全球化步伐明显提速。从“借帆出海”到“生而全球化”,中国企业实现了从低端制造出口,向技术创新和品牌先导的升级。为助力中国企业业务高效出海,亚马逊云科技于2023年6月9日在深圳大中华喜来登酒店举办…
什么样的跨网文件安全交换系统 可实现安全便捷的文件摆渡?
进入互联网时代,网络的运算和数据管理能力助力各个行业高速发展,但同样带来了一些网络安全隐患,网络攻击、数据窃取、敏感信息泄露等问题。为此,我国出台了系列政策来全面提升银各行业系统网络安全整体防护水平,其中“…
宝塔添加站点后无法访问域名的解决方法
在本地宝塔面板添加一个新的站点 如果点击域名无法访问,需要在host文件中加入该站点 window系统下的host文件路径C:\Windows\System32\drivers\etc 保存host文件后,刷新刚才的域名,即可访问本地站点。
Windows server上用nginx部署vue3项目
Windows server上用nginx部署vue3项目 一、报错信息三、总结 一、报错信息
这里,nginx给出以下错误信息: Windows:nginx: [error] CreateFile() “/logs/nginx.pid“ failed (2: The system) 经分析,造成上述错误的本…
使用Golang实现一套流程可配置,适用于广告、推荐系统的业务性框架——简单应用
在诸如广告、推荐等系统中,我们往往会涉及过滤、召回和排序等过程。随着系统业务变得复杂,代码的耦合和交错会让项目跌入难以维护的深渊。于是模块化设计是复杂系统的必备基础。这篇文章介绍的业务框架脱胎于线上多人协作开发、高并发的竞价广告系统&…
25.8 matlab里面的10中优化方法介绍—— 拉各朗日乘子法求最优化解(matlab程序)
1.简述 拉格朗日乘子法:
拉格朗日乘子法(Lagrange multipliers)是一种寻找多元函数在一组约束下的极值的方法。通过引入拉格朗日乘子,可将有 变量与 约束条件的最优化问题转化为具有变量的无约束优化问题求解
举个例子ÿ…
docker更换数据存储路径
1. 先停掉docker服务 sudo systemctl stop docker 可能会出现的问题: 这样会导致docker关闭失败,解决办法:systemctl stop docker.socket 确保docker关闭:
2.备份现在的 Docker 数据存储目录 /var/lib/docker(默认路径) mv /var/lib/docker /var/lib/…
01-1 搭建 pytorch 虚拟环境
pytorch 管网:PyTorch 一 进入 Anaconda 二 创建虚拟环境
conda create -n pytorch python3.9注意要注意断 VPN切换镜像:
移除原来的镜像
# 查看当前配置
conda config --show channels
conda config --show-sources# 移除之前的镜像
conda config --…
除了Copilot还有这些AI代码辅助工具
最近牛逼的GitHub Copilot试用到期了,离开它还有点不习惯,基础的代码它基本可以帮你搞定,开发效率直接翻倍。为啥这么好用,Copilot的背后是OpenAI和强大的GitHub代码库。那么有没有可以取代它而免费IDE的AI代码辅助工具呢…
FFmpeg常见命令行(一):FFmpeg工具使用基础
前言
在Android音视频开发中,网上知识点过于零碎,自学起来难度非常大,不过音视频大牛Jhuster提出了《Android 音视频从入门到提高 - 任务列表》。本文是Android音视频任务列表的其中一个, 对应的要学习的内容是:FFmpe…
Go -- 测试 and 项目实战
没有后端基础,学起来真是费劲,所以打算速刷一下,代码跟着敲一遍,有个印象,大项目肯定也做不了了,先把该学的学了,有空就跟点单体项目,还有该看的书....
目录
🍌单元测试…
Java课题笔记~Maven基础
2、Maven 基础
2.1 Maven安装与配置 下载安装 配置:修改安装目录/conf/settings.xml 本地仓库:存放的是下载的jar包 中央仓库:要从哪个网站去下载jar包 - 阿里云的仓库
2.2 创建Maven项目
1本Frontiers期刊不再被收录,EI期刊目录已更新 (附8月最新刊源)!
近期爱思唯尔(Elsevier)官网更新了EI Compendex收录期刊目录,这是2023年第四次更新。
Elsevier发布2023年第四版EI期刊目录
更新时间:2023年7月1日 不同于SCI/SSCI目录每月更新一次的频率,EI目录更新没有规律可言&am…
Windows同时安装两个版本的JDK并随时切换,以JDK6和JDK8为例,并解决相关存在的问题(亲测有效)
Windows同时安装两个版本的JDK并随时切换,以JDK6和JDK8为例,并解决相关存在的问题(亲测有效)
1.下载不同版本JDK
这里给出JDK6和JDK的百度网盘地址,具体安装过程,傻瓜式安装即可。
链接:http…
数学建模 好文章和资源推荐
数学建模入门篇(0基础必看,全是自己的经验) 【竞赛|数学建模】Part 1:什么是数学建模和各模块介绍 0基础小白,如何入门数学建模? 数学建模入门篇(0基础必看,全是自己的经验)
什么是数学建模
重申了一下题目ÿ…
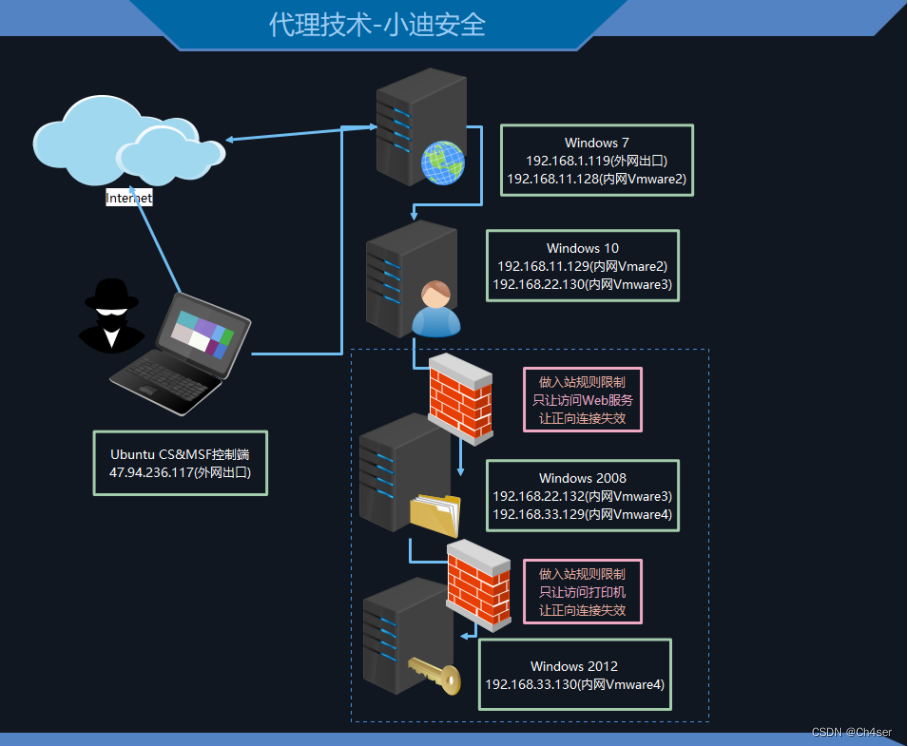
第125天:内网安全-隧道技术SMBICMP正反向连接防火墙出入规则上线
知识点
#知识点:
1、入站规则不出网上线方案
2、出站规则不出网上线方案
3、规则-隧道技术-SMB&ICMP-隧道技术:解决不出网协议上线的问题(利用出网协议进行封装出网)
-代理技术:解决网络通讯不通的问题࿰…