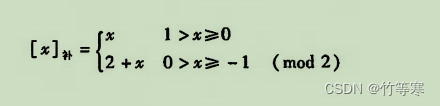本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/132915.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
【sgDragMoveTile】自定义组件:拖拽瓦片图、地图、大图,滚动条对应同步滚动
特性: 可以自定义拖拽过程鼠标样式可以禁止拖拽动态设置拖拽和滚动区域元素 sgDragMoveTile源码
<template><div :class"$options.name"> </div>
</template>
<script>
export default {name: sgDragMoveTile,data() {ret…
热烈祝贺埃文科技代码特工队斩获2023黄河鲲鹏开发者大赛河南赛区创新赛道二等奖
2023年9月19日,由河南省教育厅、黄河科技集团有限公司、华为技术有限公司联合主办,郑州中原科技城管理委员会、中原鲲鹏生态创新中心联合承办的2023黄河鲲鹏开发者大赛河南区域决赛圆满落幕。
决赛中,来自企业和高校的121支团队,…
SpringMVC 学习(七)JSON
9. JSON
9.1 简介
JSON(JavaScript Object Notation,JS 对象标记)是一种轻量级数据交换格式,采用独立于编程语言的文本格式储存和表示数据,易于机器解析和生成,提升网络传输效率。
任何 JavaScript 支持…
Serverless 数仓技术与挑战(内含 PPT 下载)
近期,Databend Labs 联合创始人张雁飞发表了题为「Serverless 数仓技术与挑战」的主题分享。以下为本次分享的精彩内容: 主题: 「Serverless 数仓技术与挑战」
演讲嘉宾: 张雁飞
嘉宾介绍: Databend Labs 联合创始人…
竞赛 基于深度学习的动物识别 - 卷积神经网络 机器视觉 图像识别
文章目录 0 前言1 背景2 算法原理2.1 动物识别方法概况2.2 常用的网络模型2.2.1 B-CNN2.2.2 SSD 3 SSD动物目标检测流程4 实现效果5 部分相关代码5.1 数据预处理5.2 构建卷积神经网络5.3 tensorflow计算图可视化5.4 网络模型训练5.5 对猫狗图像进行2分类 6 最后 0 前言
&#…
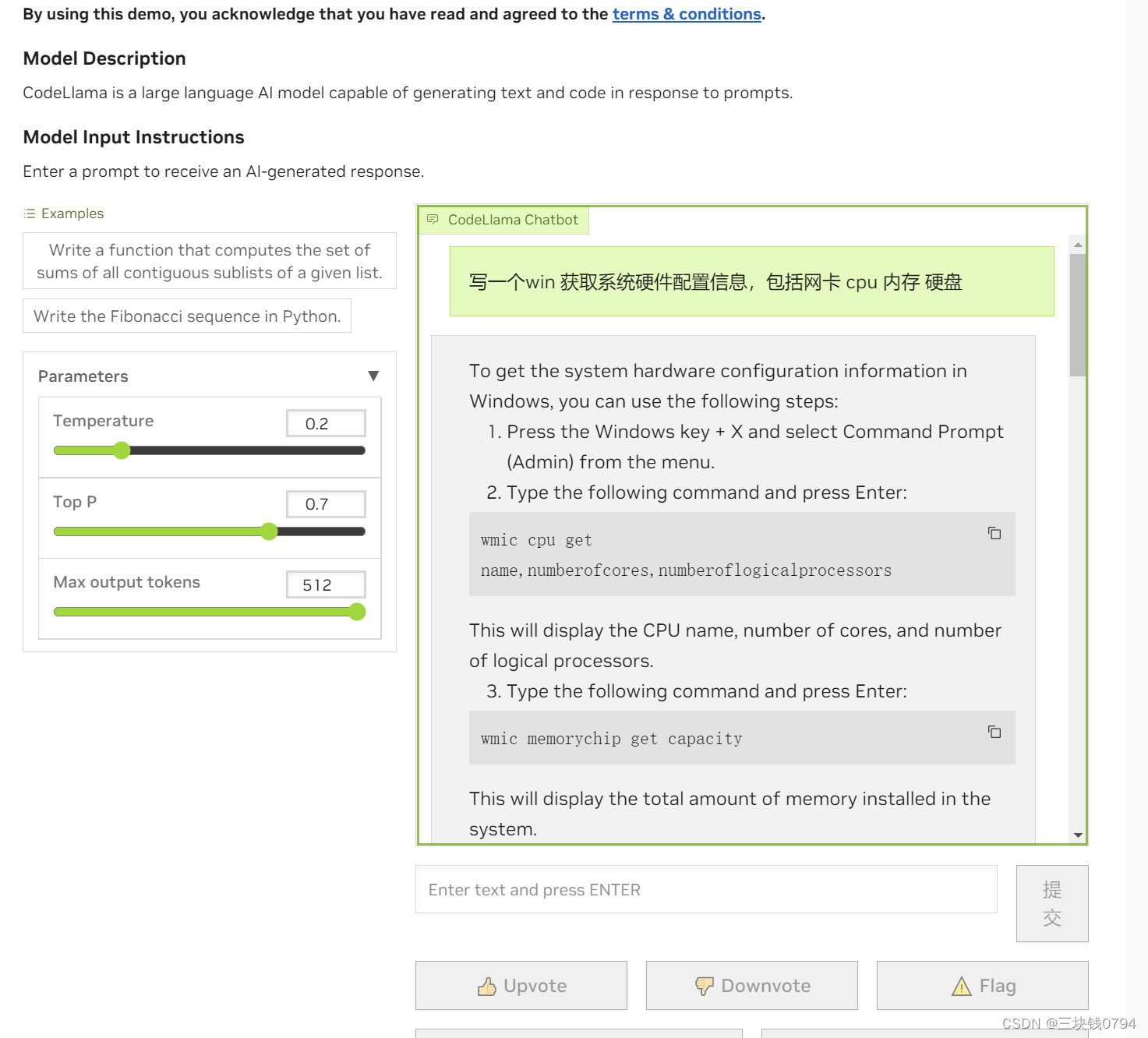
英伟达 nvidia 官方code llama在线使用
新一代编程语言模型Code Llama面世:重新定义编程的未来
随着人工智能和机器学习技术的迅速发展,我们现在迎来了一款革命性的大型编程语言模型——Code Llama。该模型是基于Llama 2研发的,为开放模型中的佼佼者,其性能达到了行业领…
如何重装Windows Mirosoft Store
重装Windows Mirosoft Store 如何重装Windows Mirosoft Store呢?如何下载Windows Mirosoft Store呢?Windows Mirosoft Store不见了咋办?Windows 自带软件不见了咋办等等?写在前面 1.文件准备2.安装 如何重装Windows Mirosoft Stor…
数据大爆炸:大数据分析如何改变我们的世界
文章目录 大数据分析的基本概念数据的三个V大数据分析的技术 大数据分析在商业中的应用1. 个性化营销2. 风险管理3. 供应链优化4. 客户服务 大数据分析在医疗保健中的应用1. 疾病预测2. 患者治疗3. 医疗设备监控 大数据分析在科学研究中的应用1. 天文学2. 生物学3. 气象学 大数…
Python | 为FastAPI后端服务添加API Key认证(分别基于路径传参和header两种方式且swagger文档友好支持)
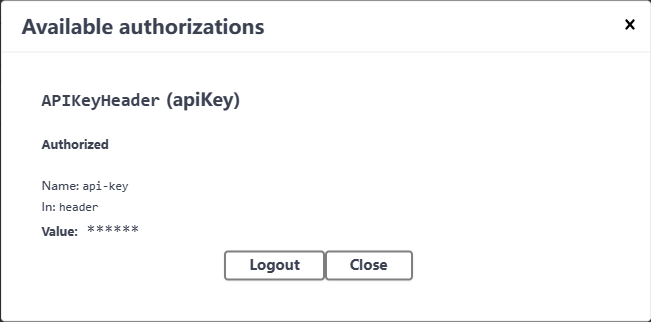
文章目录 01 前言02 路径传参方式添加API Key2.1 完整代码2.2 请求示例2.3 swagger文档测试 03 请求头Header方式传入API Key(推荐)3.1 完整代码3.2 请求示例3.3 swagger文档测试 01 前言
FastAPI,如其名所示,是一个极为高效的框…
react版音乐播放器的各种兼容问题
由于工作要求,需要制作一个h5页面的音乐播放器,其实如果放在原生做,效果会好很多,其实大多数app的音乐播放器也是原生做的,所以会要求你打开app再去播放音乐,但是有些特殊的情况,还是会用到h5播…
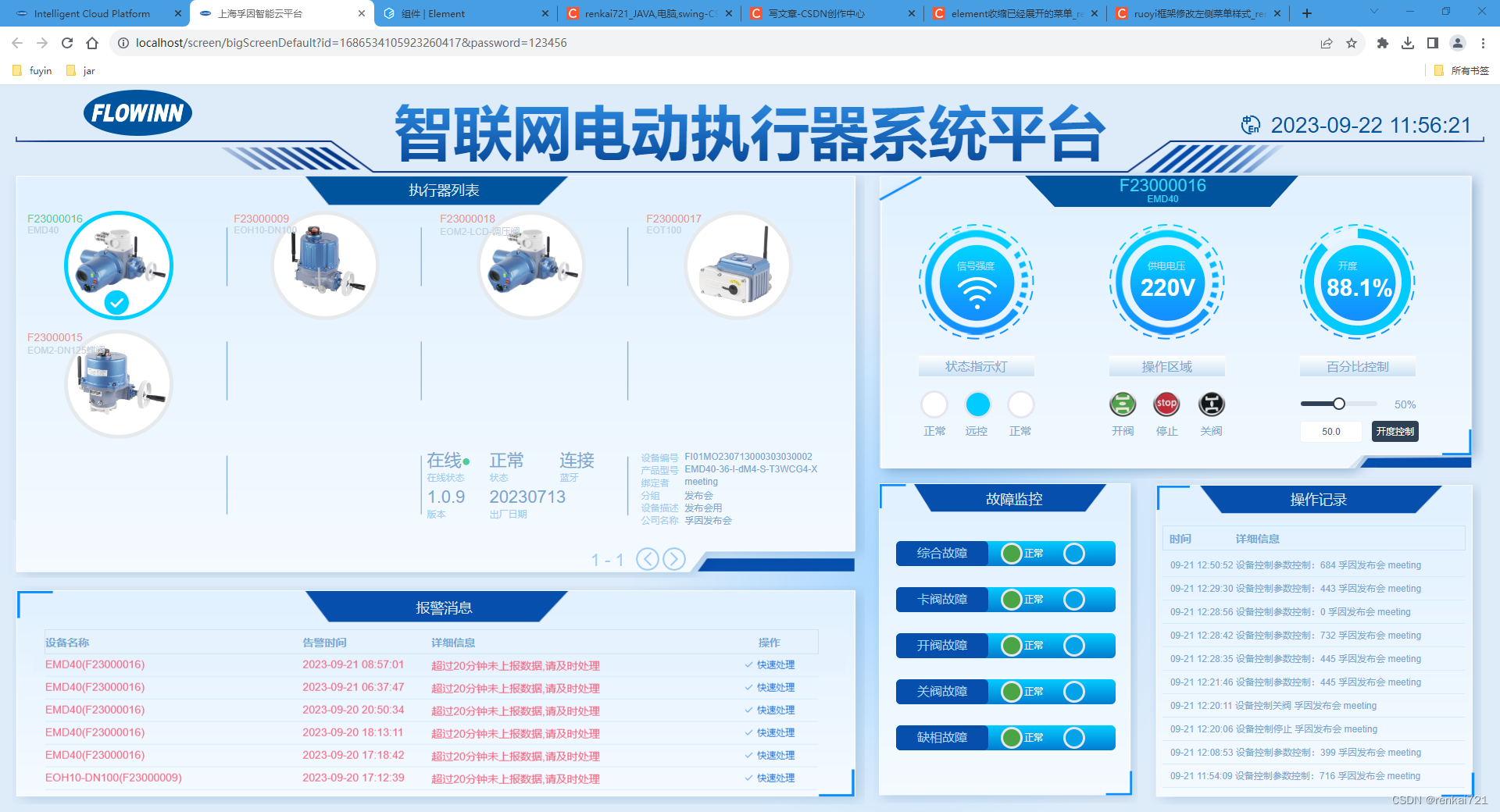
ruoyi框架开发LOT项目
背景
最近闲着就用ruoyi的框架写了一个LOT项目,个人觉得效果还可以。
1、首页 2、企业管理 3、用户管理 4、设备列表 5、设备列表标签展示 6、设备详情页面 7、大屏展示界面 8、结束
-----华丽的分割线,以下是凑字数,大家不用花时间看&…
Linux系统之links和elinks命令的基本使用
Linux系统之links和elinks命令的基本使用 一、links与elinks命令介绍1. links命令简介2. elinks命令简介 二、links与elinks命令区别三、links命令选项解释四、links命令的基本使用1. links安装2. 查看links版本3. 图形模式打开网址4. 直接使用links命令5. 打印url版本到标准格…
【sgUploadTileImage】自定义组件:浏览器端生成瓦片图,并转换为File文件序列上传瓦片图
特性: 支持自定义瓦片图尺寸支持显示预览最小尺寸100x100像素大小,切换为实际切割尺寸支持获取切割后的文件Files数组 sgUploadTileImage源码
<template><div :class"$options.name"><div class"sg-ctrl"><di…
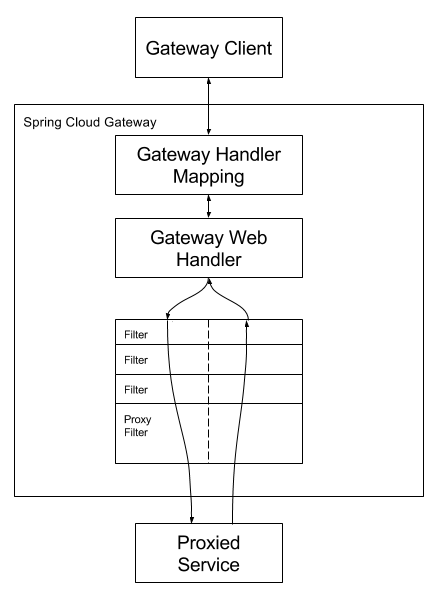
Springboot: Spring Cloud Gateway 使用的基本概念及配置介绍
1. SpringCloud 与 SpringBoot的版本映射关系
在已有的Spring Boot项目中增加Spring Cloud,首先要确定使用的Spring Cloud的版本,这取决于项目使用的Spring Boot的版本 SpringCloud 与 SpringBoot的版本映射关系
如果两者的版本不兼容,再会…
python算法部署(通信篇)
1.dockerflask方式
# YOLOv5 🚀 by Ultralytics, AGPL-3.0 license
"""
Run a Flask REST API exposing one or more YOLOv5s models
"""import argparse
import io
import jsonimport torch
from flask import Flask, jsonify, req…
SpringCloud 学习(四)Hystrix
6. Netflix.Hystrix
6.1 简介
● 扇出
多服务之间调用,若微服务 A 调用微服务 B 和微服务 C,微服务 B 和 微服务 C 又调用其他微服务,这就是扇出
● 服务雪崩
若扇出的链路上某个微服务的调用响应时间过长或者不可用,么此扇出…
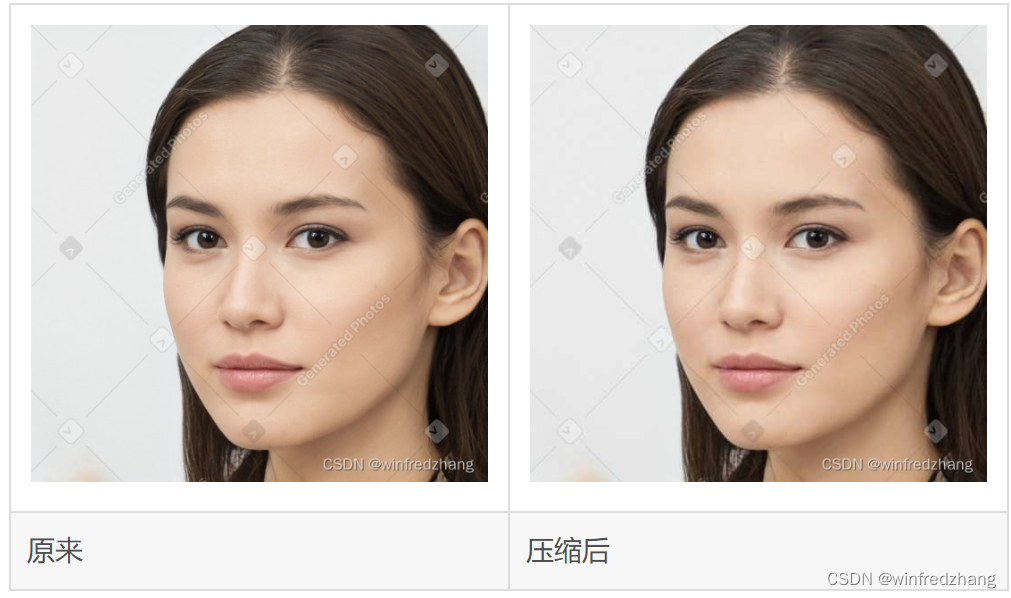
Python编程:使用PIL进行JPEG图像压缩的简易教程
摘要: 本文介绍了如何使用Python编程语言和wxPython图形用户界面库进行JPEG图像的压缩。通过添加滑块控件,我们可以调整压缩质量,并将压缩后的照片另存为原来的名称加上后缀"压缩质量数字"的新文件。 C:\pythoncode\new\image2small.py 完整…
学习:原码-反码-补码
文章目录 前提知识原码详解反码补码 二进制负数的运算 前提知识
正数不需要进行原码反码补码一说,正数就是正数,我们原码反码补码是为了针对负数 (按道理来说其实根本不存在什么码,只有二进制机器码,不过是为了方便计…