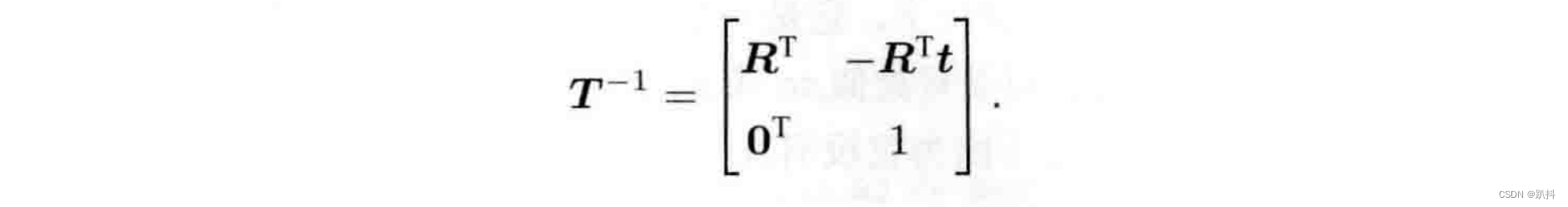本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/238108.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Selenium安装WebDriver最新Chrome驱动(含116/117/118/119)
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…
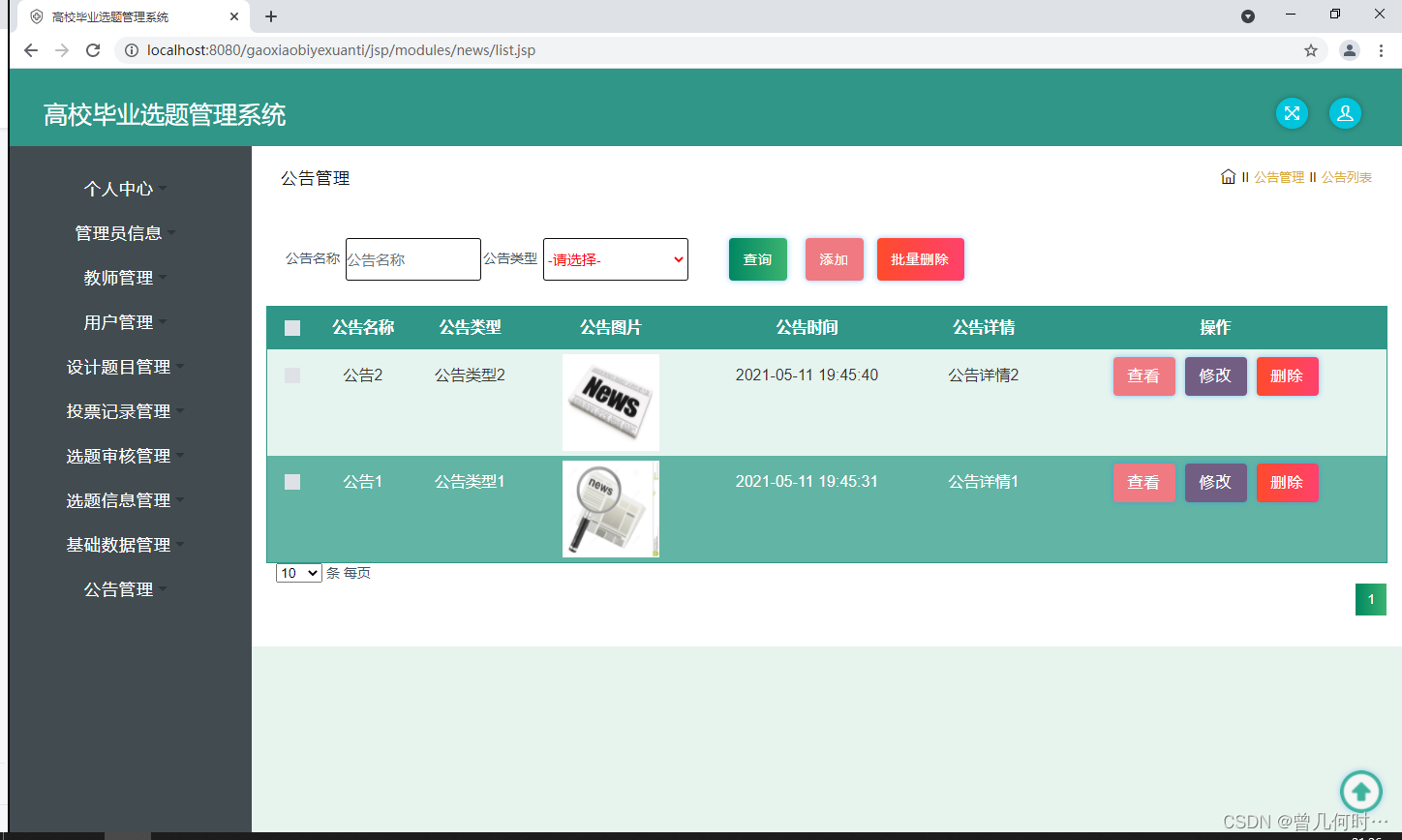
基于SSM的高校毕业选题管理系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…
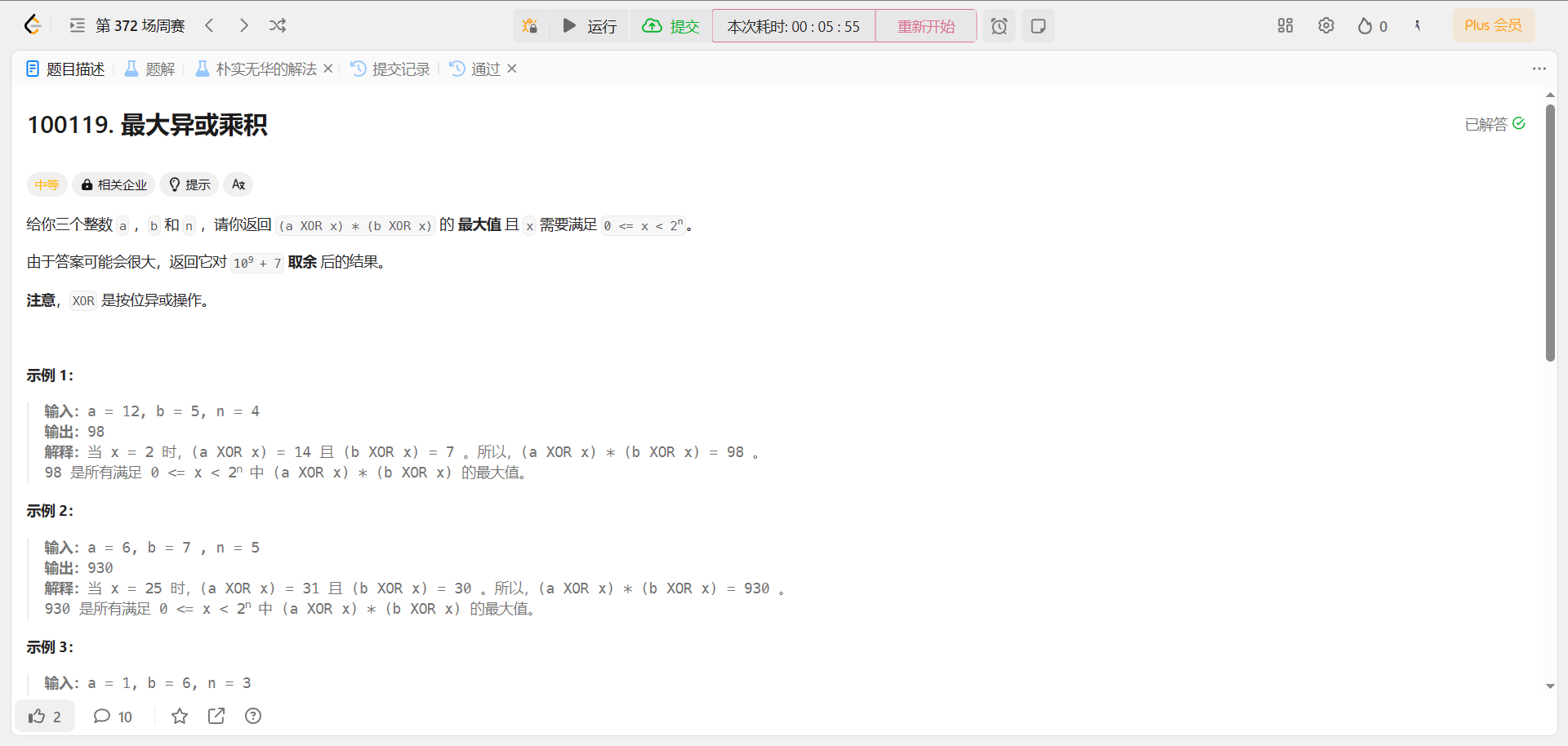
力扣周赛372 模拟 思维 位运算 java
100131. 使三个字符串相等 ⭐ AC code
class Solution {public int findMinimumOperations(String s1, String s2, String s3) {int len1 s1.length();int len2 s2.length();int len3 s3.length();int n Math.min(len1,len2);n Math.min(n,len3);int i 0;while(i < n…
网站被攻击怎么办?德迅云安全SCDN为您保驾护航
安全加速(Secure Content Delivery Network,SCDN)是德迅云安全推出的集分布式DDoS防护、CC防护、WAF防护、BOT行为分析为一体的安全加速解决方案。已使用内容分发网络(CDN)或全站加速网络(ECDN)…
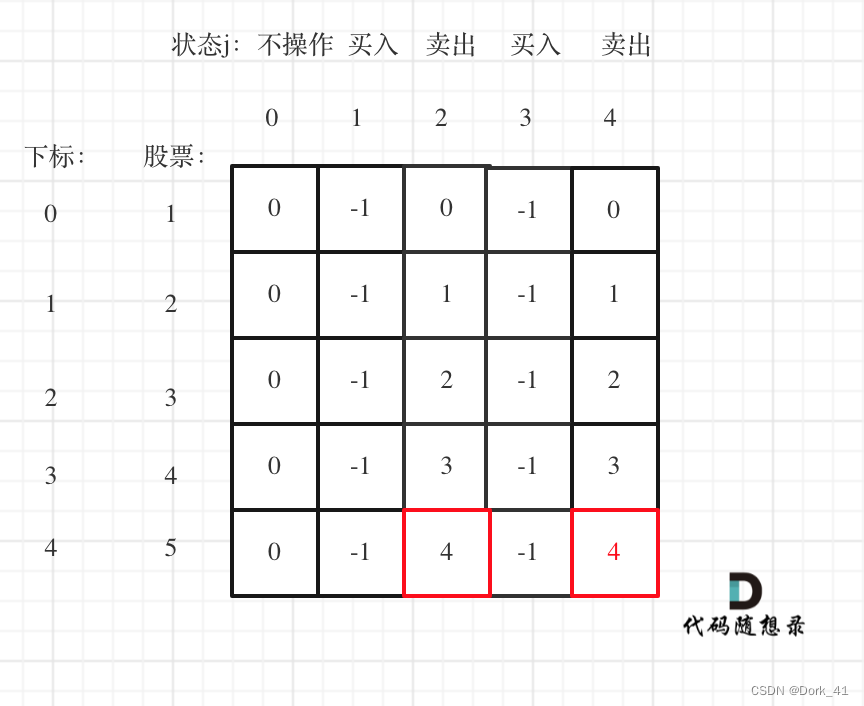
代码随想录算法训练营第四十九天| 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
文档讲解:代码随想录 视频讲解:代码随想录B站账号 状态:看了视频题解和文章解析后做出来了 123.买卖股票的最佳时机III
class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices) 0:return 0dp [[0] * 5 for _ in…
如何判断sql注入流量特征
如何判断sql注入流量特征
以dvwa的sql注入为例
首先构造一个完整的sql注入请求包
GET /dvwa_2.0.1/vulnerabilities/sqli/?id1&SubmitSubmit HTTP/1.1
Host: 10.9.47.41
User-Agent: Mozilla/5.0 (Windows NT 10.0; Win64; x64; rv:109.0) Gecko/20100101 Firefox/119.…
解析Spring Boot中的CommandLineRunner和ApplicationRunner:用法、区别和适用场景详解
在Spring Boot应用程序中,CommandLineRunner和ApplicationRunner是两个重要的接口,它们允许我们在应用程序启动后执行一些初始化任务。本文将介绍CommandLineRunner和ApplicationRunner的区别,并提供代码示例和使用场景,让我们更好…
【视觉SLAM十四讲学习笔记】第三讲——旋转矩阵
专栏系列文章如下: 【视觉SLAM十四讲学习笔记】第一讲——SLAM介绍 【视觉SLAM十四讲学习笔记】第二讲——初识SLAM 本章将介绍视觉SLAM的基本问题之一:如何描述刚体在三维空间中的运动? 旋转矩阵
点、向量和坐标系 三维空间由3个轴组成&…
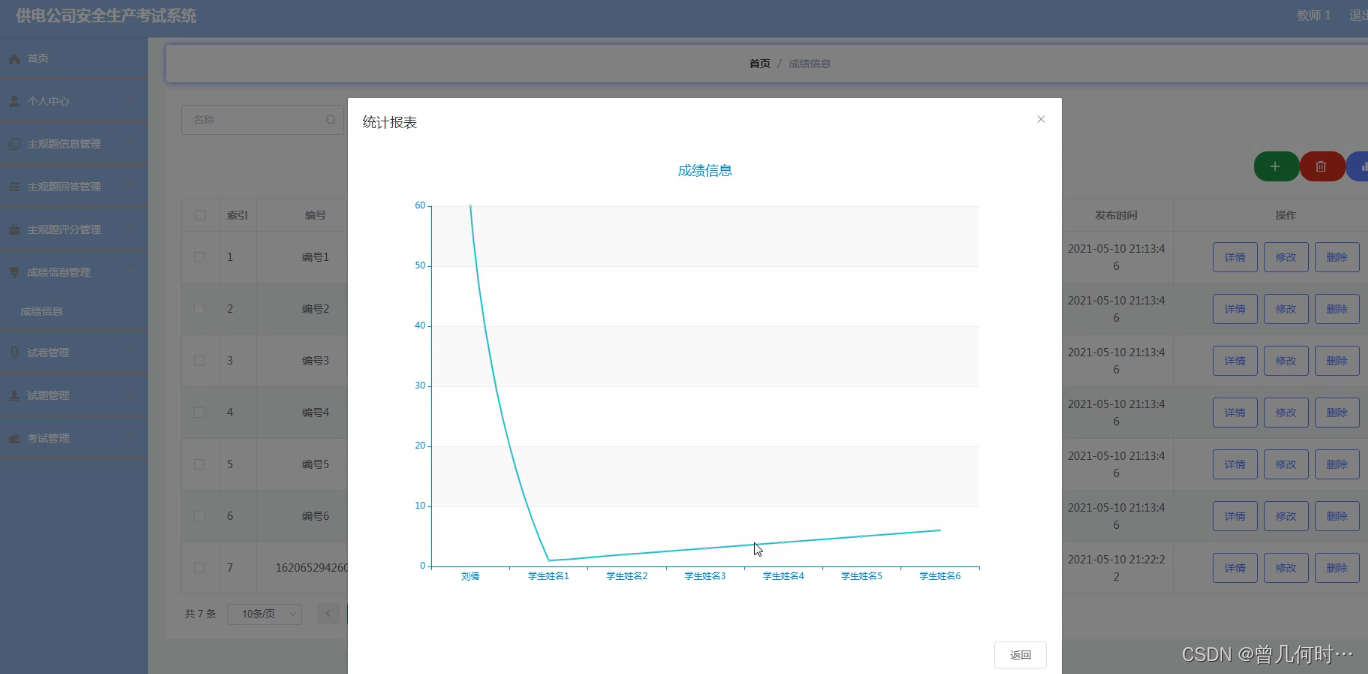
基于SSM的供电公司安全生产考试系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…
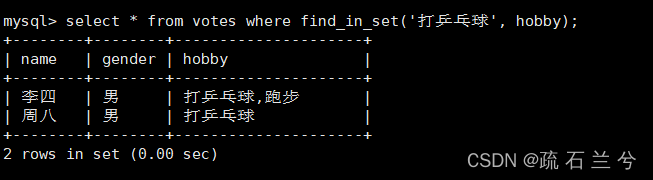
细说MySQL数据类型
TOC
目录 MySQL数据类型
数据类型分类
数值类型
tinyint类型
有符号tinyint范围测试
无符号tinyint范围测试
bit类型
bit类型的显示方式
bit类型的范围测试
float类型
有符号float范围测试
无符号float范围测试
decimal类型
字符串类型
char类型
char类型测试 …
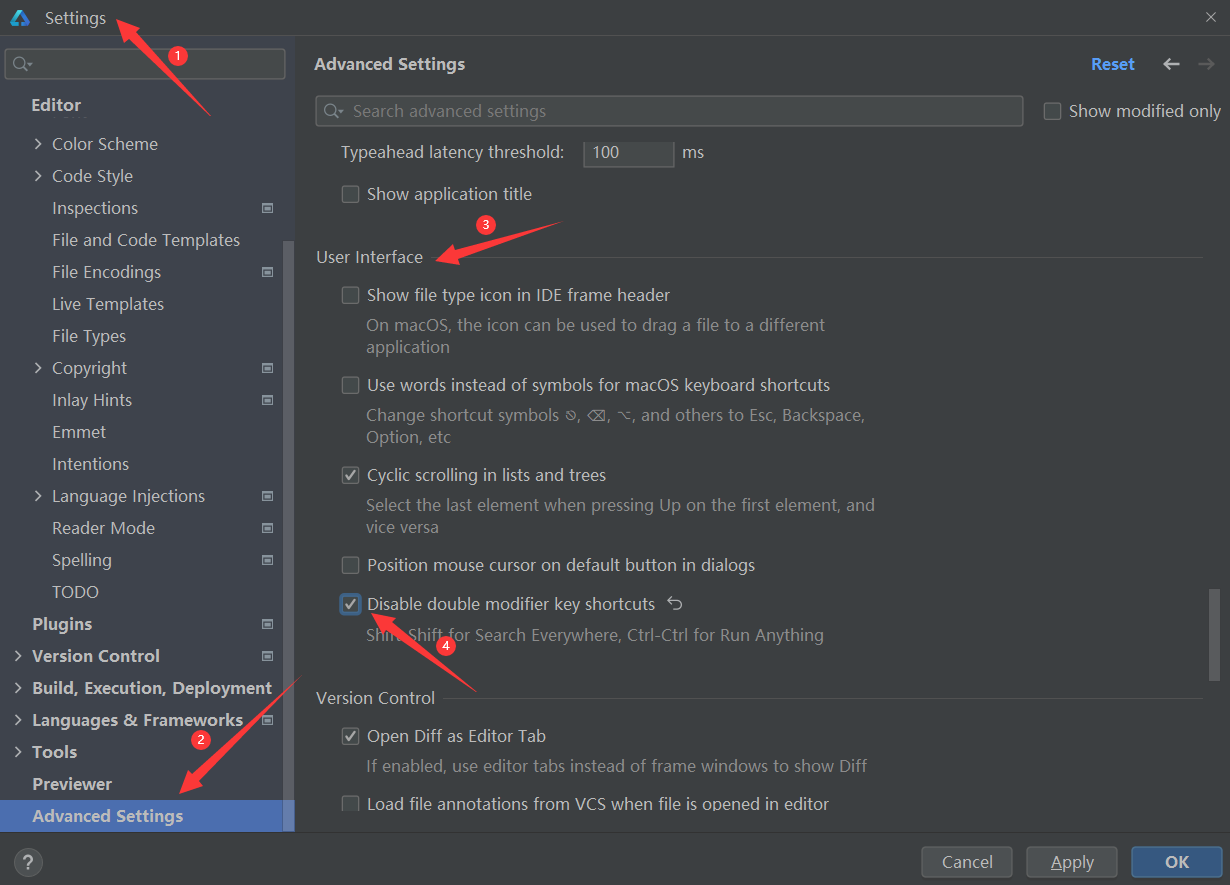
鸿蒙4.0开发笔记之DevEco Studio之配置代码片段快速生成(三)
一、作用
配置代码片段可以让我们在Deveco Studio中进行开发时快速调取常用的代码块、字符串或者某段具有特殊含义的文字。其实现方式类似于调用定义好变量,然而这个变量是存在于Deveco Studio中的,并不会占用项目的资源。
二、配置代码段的方法
1、打…
【JavaEE初阶】 CSS相关属性,元素显示模式,盒模型,弹性布局,Chrome 调试工具||相关讲解
文章目录 🎋字体属性🚩设置字体🚩字体大小🚩字体粗细🚩文字样式 🎍文本属性🚩文本颜色🎈认识 RGB🎈设置文本颜色 🚩文本对齐🚩文本装饰Ƕ…
趣学python编程 (五、常用IDE环境推荐)
Python环境指的是在计算机上安装Python解释器和相关的库,它是运行Python代码所必需的。那么开始Python编程前,准备安装好开发环境是前提。 默认的电脑上只是让人办公使用的,不带python编程开发环境。只有安装python环境,才可以编写…
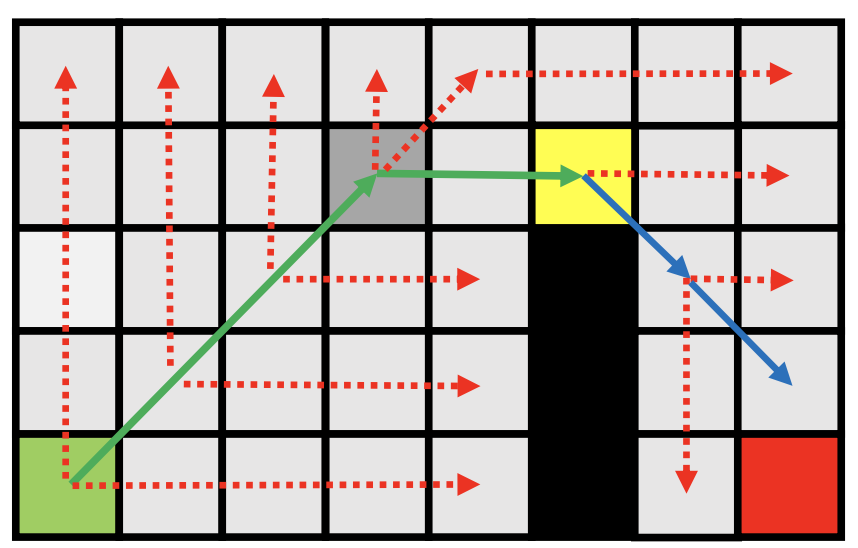
Motion Plan之搜素算法笔记
背景:
16-18年做过一阵子无人驾驶,那时候痴迷于移动规划;然而当时可学习的资料非常少,网上的论文也不算太多。基本就是Darpa的几十篇无人越野几次比赛的文章,基本没有成系统的文章和代码讲解实现。所以对移动规划的认…
车载通信架构 —— 新车载总线类型下(以太网)的通信架构
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。
老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不…
Wordpress多语言插件:WPML插件使用教程,最佳的多语言建站方案
今天小编讲的是另外一款多语言插件WPML。相比Gtranslate采用的是机器翻译,难免存在翻译不准确,词不达意的情况,WPML可以支持人工翻译内容添加。 事先说明一点:用插件实现多语言较为方便,但此方法做出的多语言网站SEO性能一般,只建议展示站使用,如果想要SEO营销型多语言网…
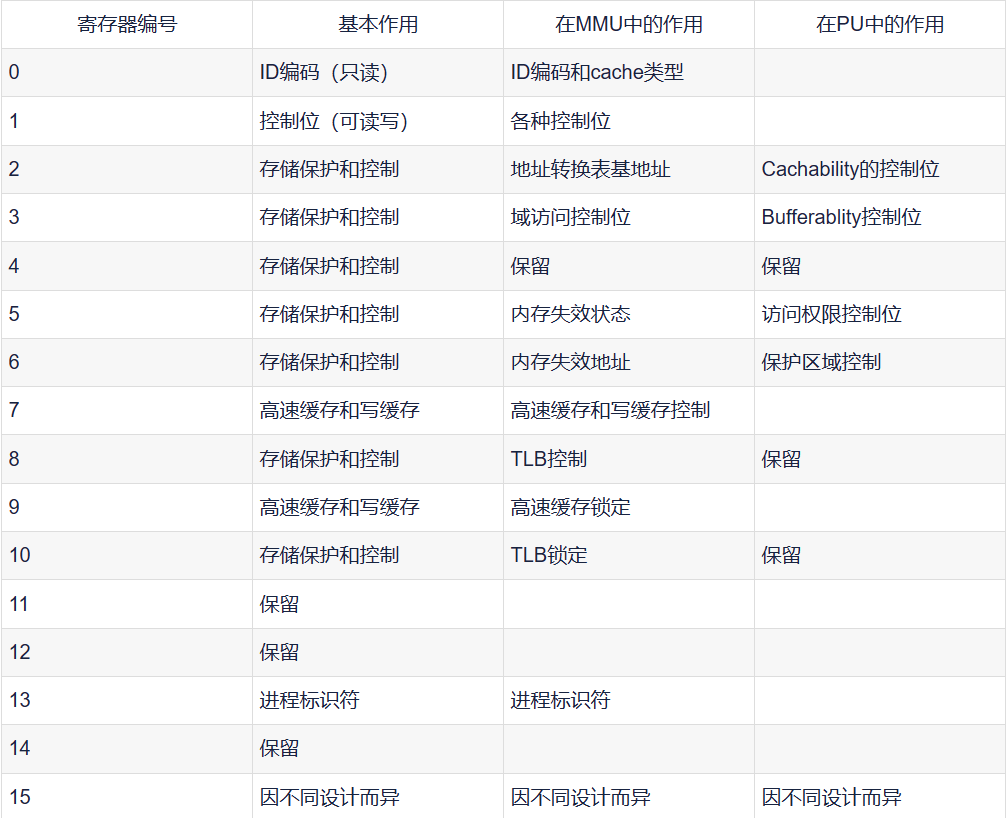
U-boot(三):start.S
本文主要探讨x210的uboot的start.S文件,也是uboot启动的第一阶段。
头文件 config.h config.h x210_sd.h,由mkconfig脚本生成,包含了开发板的配置宏
rootkaxi-virtual-machine:~/qt_x210v3s_160307/uboot/include# cat config.h
/* Automatically generate…
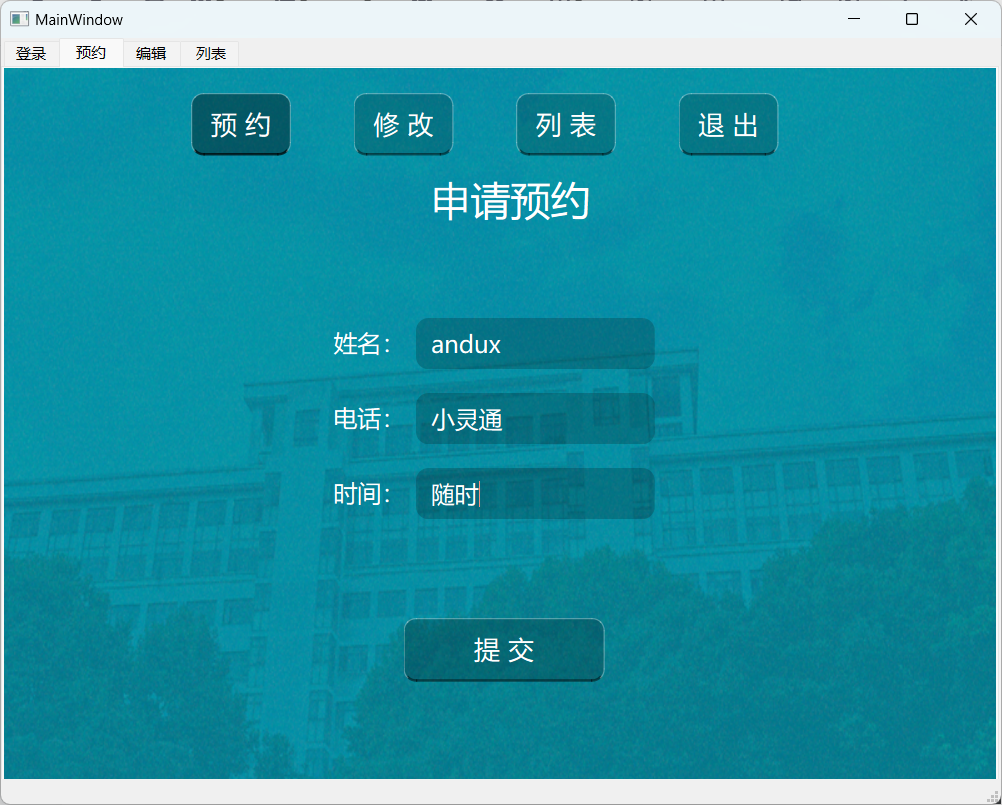
pyinstaller 打包pyqt6等ui文件为exe可执行程序的方法
刚开始使用auto-py-to-exe打包pyqt6的程序,折腾好半天都会出错,关键打包出来的exe单文件有快100兆了,真大啊!
auto-py-to-exe有图形界面,看起来比较直观。 还有中文语言,对使用者比较友善,可以…
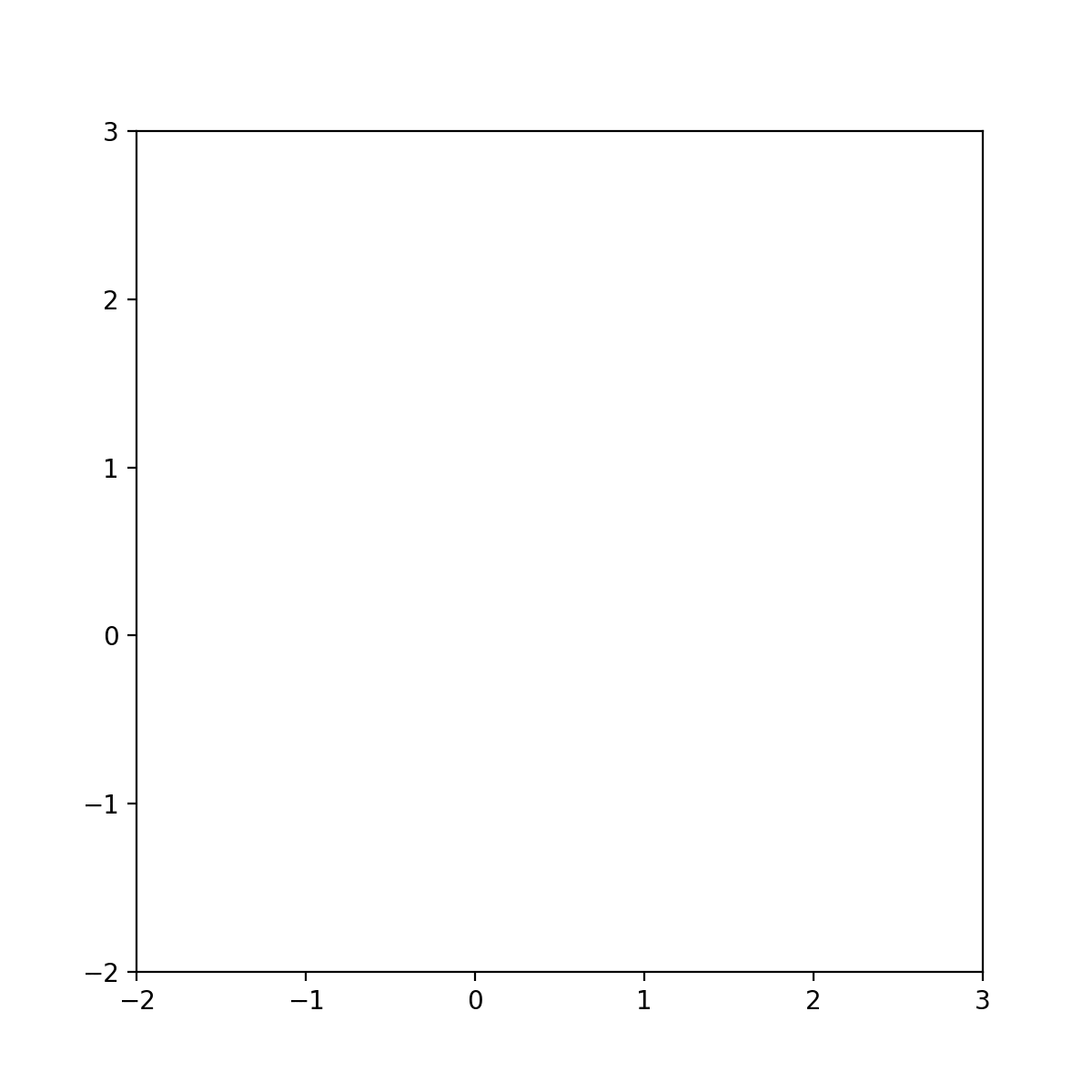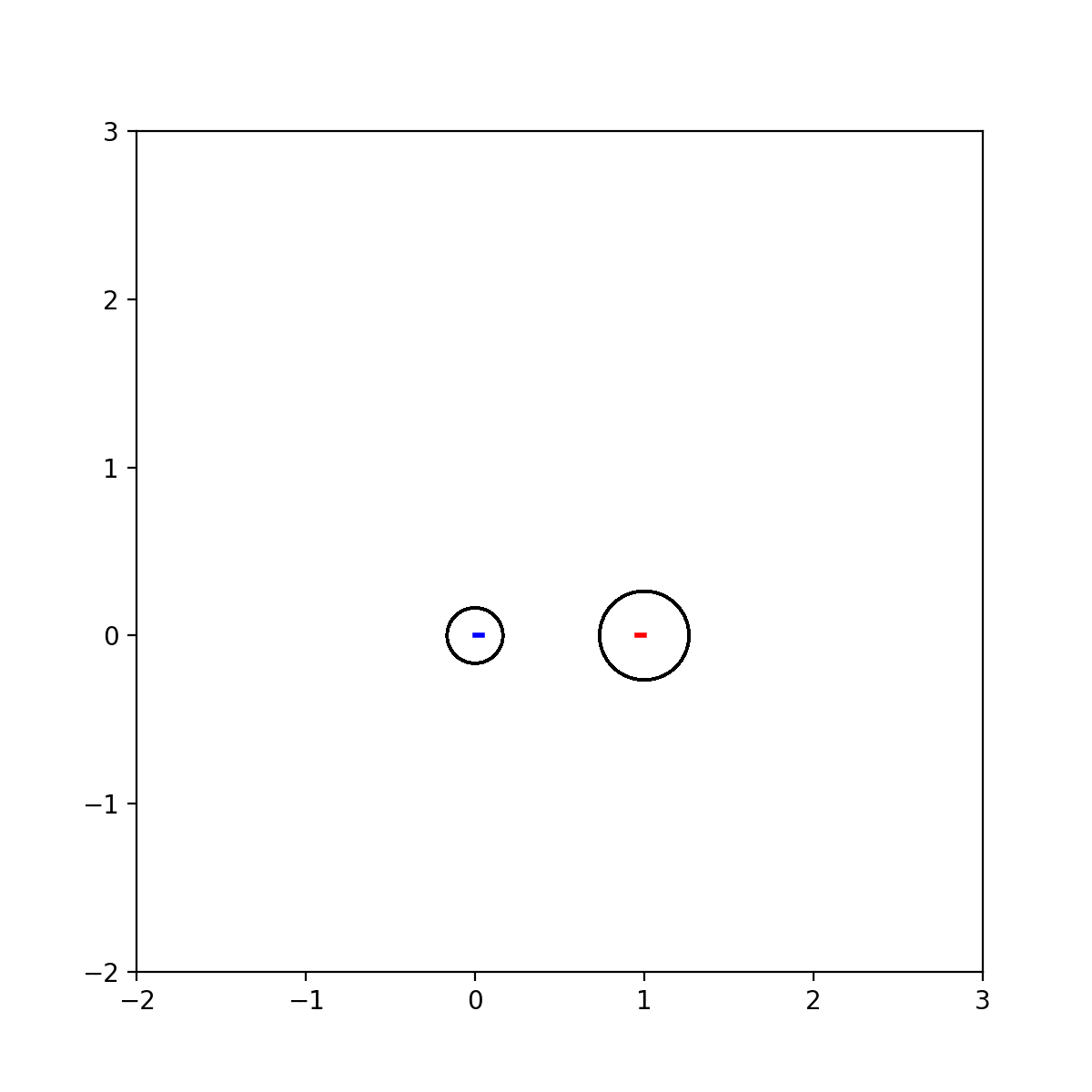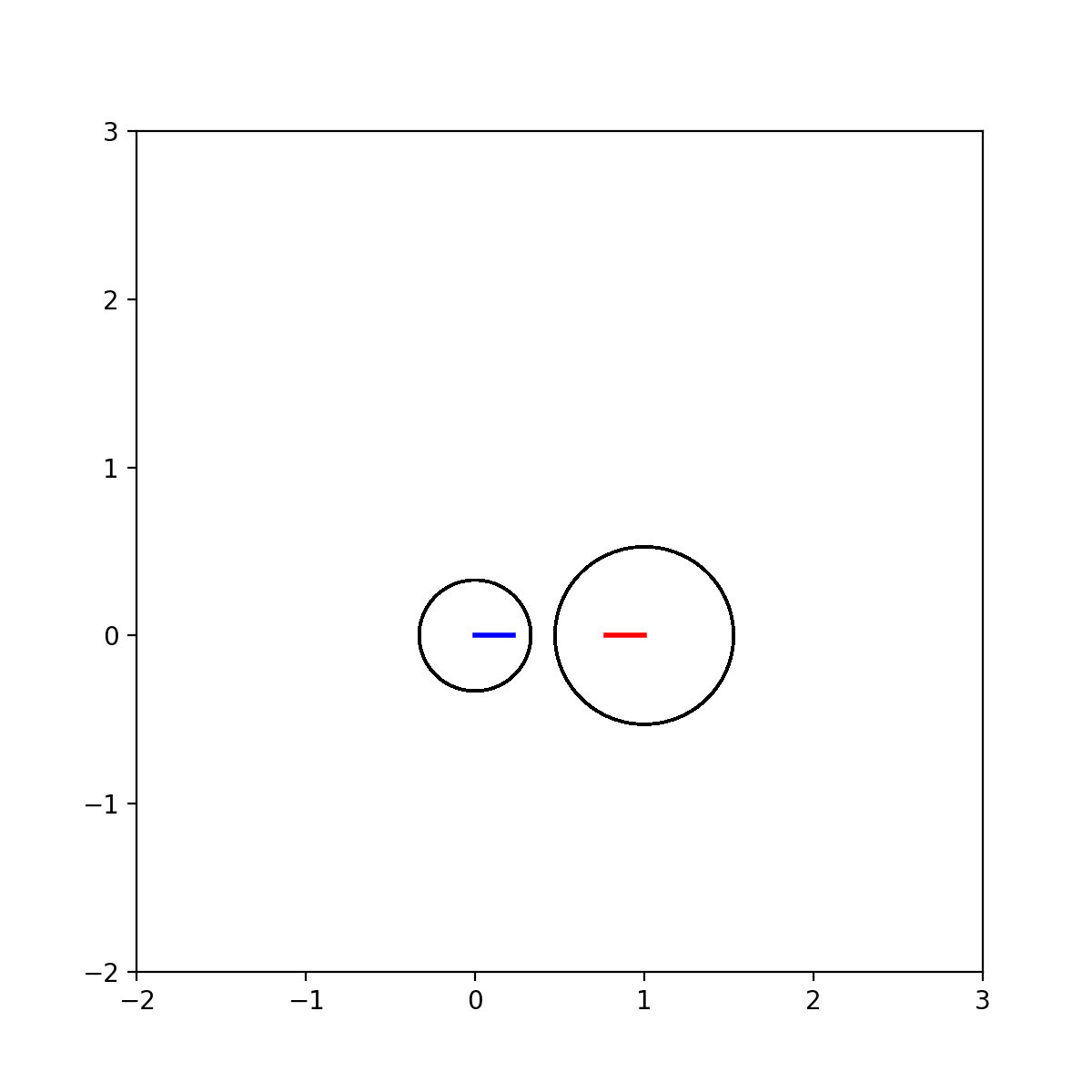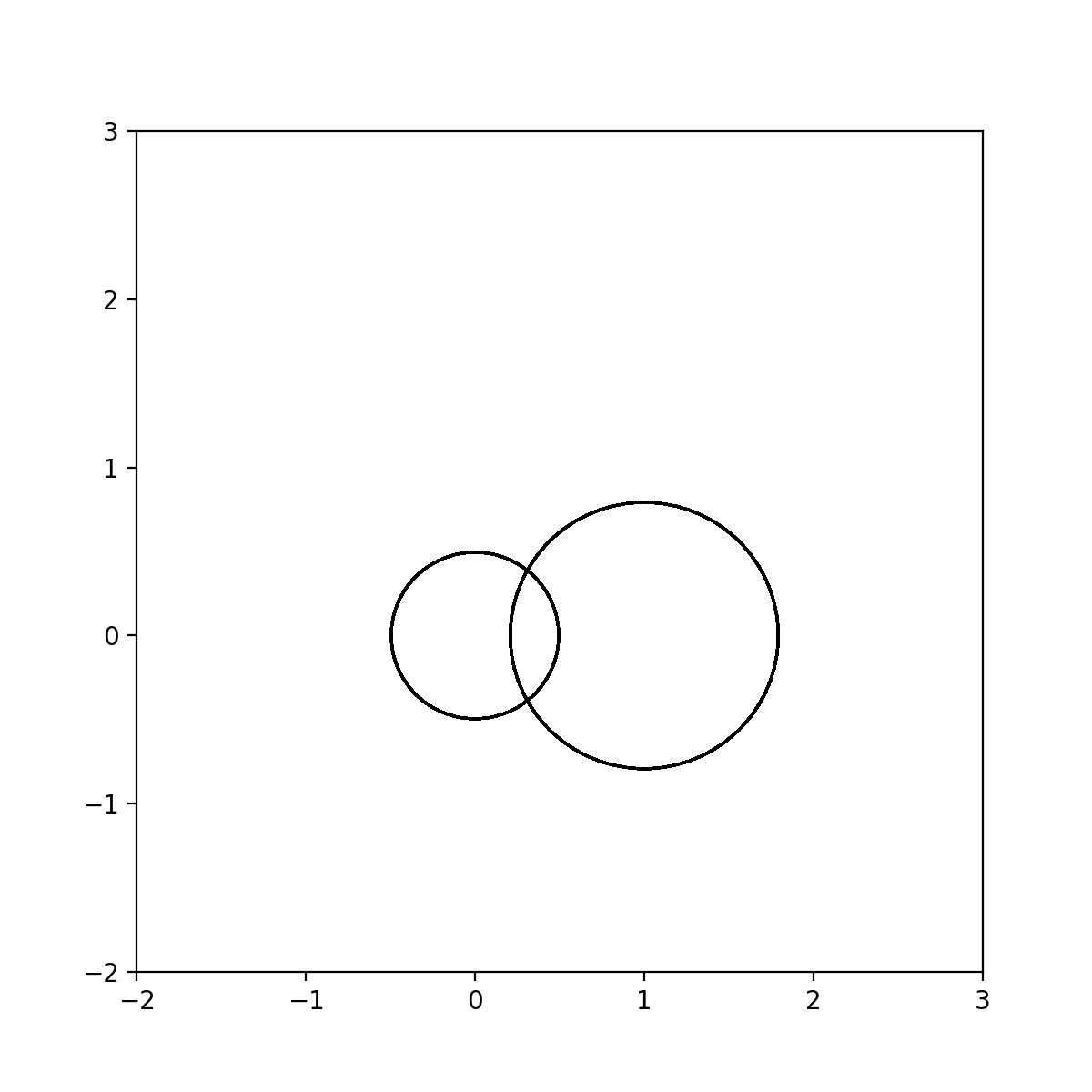
矩阵理论——Gerschgorin定理,以及用python绘制Gerschgorin圆盘动图
矩阵理论——Gerschgorin定理,以及用python绘制Gerschgorin圆盘动图
在矩阵的特征值估计理论当中,有一节是盖尔圆盘定理: 对于一个n阶复数矩阵A,每个特征值lambda位于至少一个Gerschgorin圆盘中,这些圆盘的中心为矩阵…