本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/311175.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
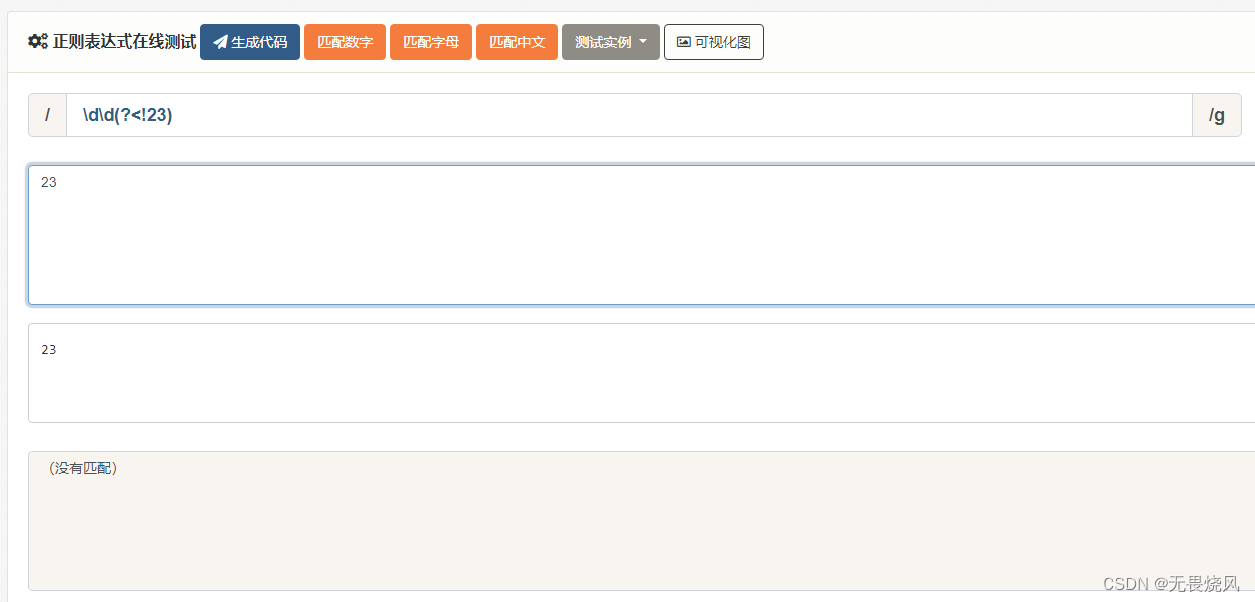
正则表达式匹配 int unint uint16 类型最大值最小值的类型范围
以int16来举例
答案
^([1-6]\d(?<!6[6-9])\d(?<!65[6-9])\d(?<!655[4-9])\d(?<!6553[6-9])|0|10{4}|[1-9]\d{0,3})$解析
int16的范围是 0~65535 。我们把它分解为 0 1~9999 10000 ~ 65535 。前两组很简单如下
0[1-9]\d{0,3}正则表达式 否定式向后查看
(?…
ubuntu安装node
1 下载
node 官网下载 如果需要其他版本,点击上图的Other Downloads 这里下载的版本是20.11.0 Linux Binaries (x64),下载下来后是node-v20.11.0-linux-x64.tar.xz这样的格式,直接右键解压得到如下目录: 直接拷贝该文件夹到指定目…
流量预测中文文献阅读(郭郭专用)
目录 基于流量预测的超密集网络资源分配策略研究_2023_高雪亮_内蒙古大学(1)内容总结(2)流量预测部分1、数据集2、结果对其中的一个网格的CDR进行预测RMSE和R2近邻数据和周期数据对RMSE的影响 (3)基于流量预…
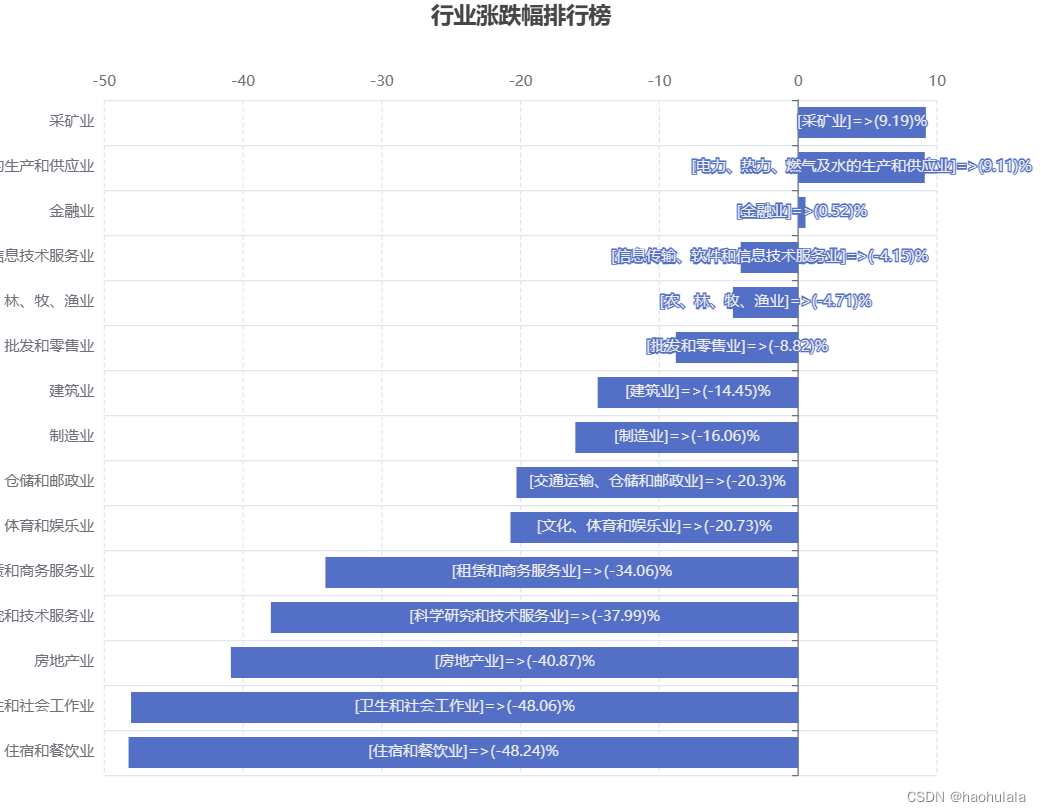
【金融数据分析】计算2023年沪深300行业涨跌幅
本文我们来计算2023年沪深300行业涨跌幅,最后呈现的页面是这样的 先来说后端的代码,计算行业涨跌幅的原理就是将某个行业所有成分股的涨跌幅加起来,然后除以股票数量得到一个平均涨跌幅 // 查询行业涨跌幅public List<CSI300IndustryRankV…
基于SSM+vue的新生报到服务管理系统(Java毕业设计)
大家好,我是DeBug,很高兴你能来阅读!作为一名热爱编程的程序员,我希望通过这些教学笔记与大家分享我的编程经验和知识。在这里,我将会结合实际项目经验,分享编程技巧、最佳实践以及解决问题的方法。无论你是…
Leetcode 494 目标和
题意理解: 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添…
代码随想录算法训练营第32天|122.买卖股票的最佳时机II 55. 跳跃游戏 45.跳跃游戏II
122.买卖股票的最佳时机II
class Solution {
public:int maxProfit(vector<int>& prices) {int result 0;for (int i 1; i < prices.size(); i) {result max(prices[i] - prices[i - 1], 0);}return result;}
}; 思路太重要了 图片来源:转载自代码…
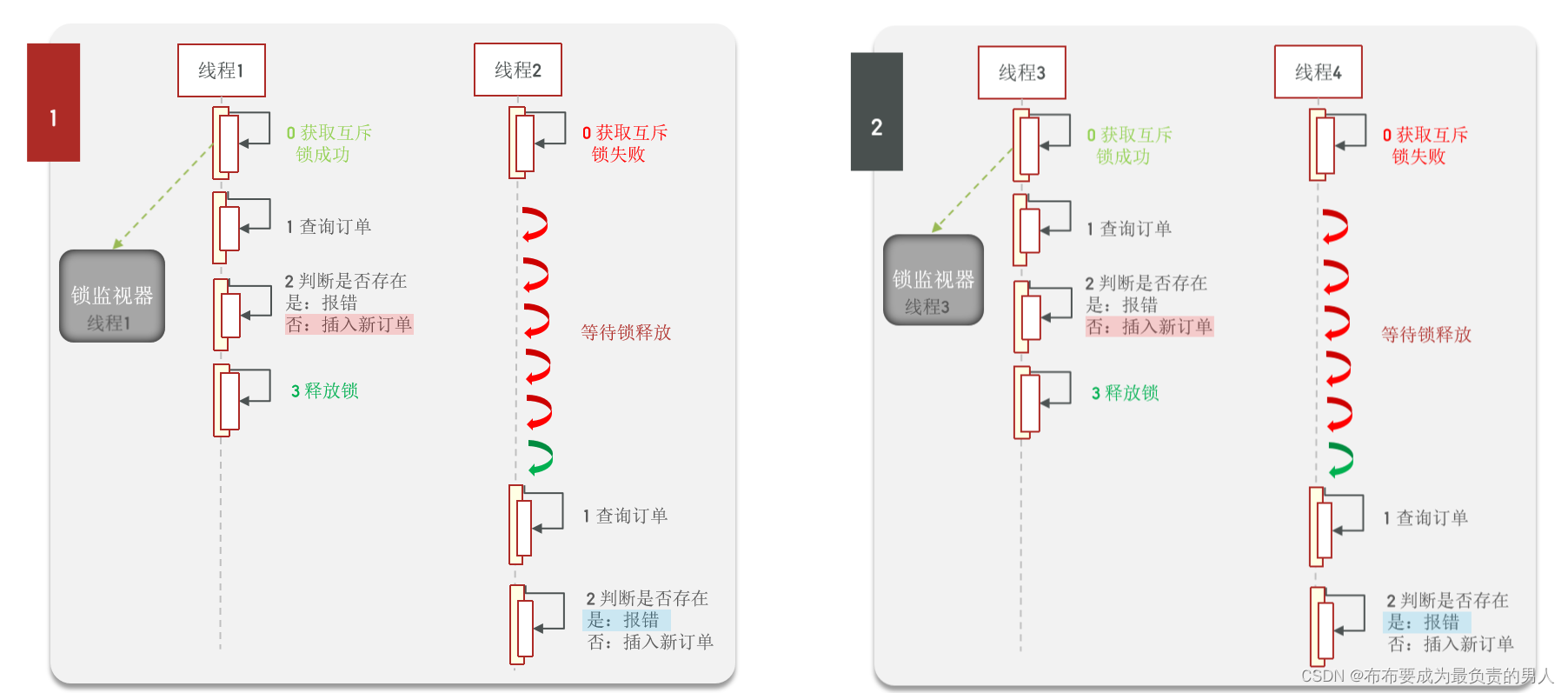
Redis:原理速成+项目实战——Redis实战7(优惠券秒杀+细节解决超卖、一人一单问题)
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理速成项目实战——Redis实战6(封装缓存工具(高级写法)&&缓存总…
麒麟操作系统缓存rpm包,制作离线yum源
缓存rpm包,以make为例
mkdir -p /data/yum
yumdownloader --resolve --destdir/data/yum make制作离线yum包
yum install createrepo -y
cd /data/yum
createrepo .写yum配置文件/etc/yum.repos.d/local.repo
[local-repo]
namelocal-repo
baseurlfile:///data/…
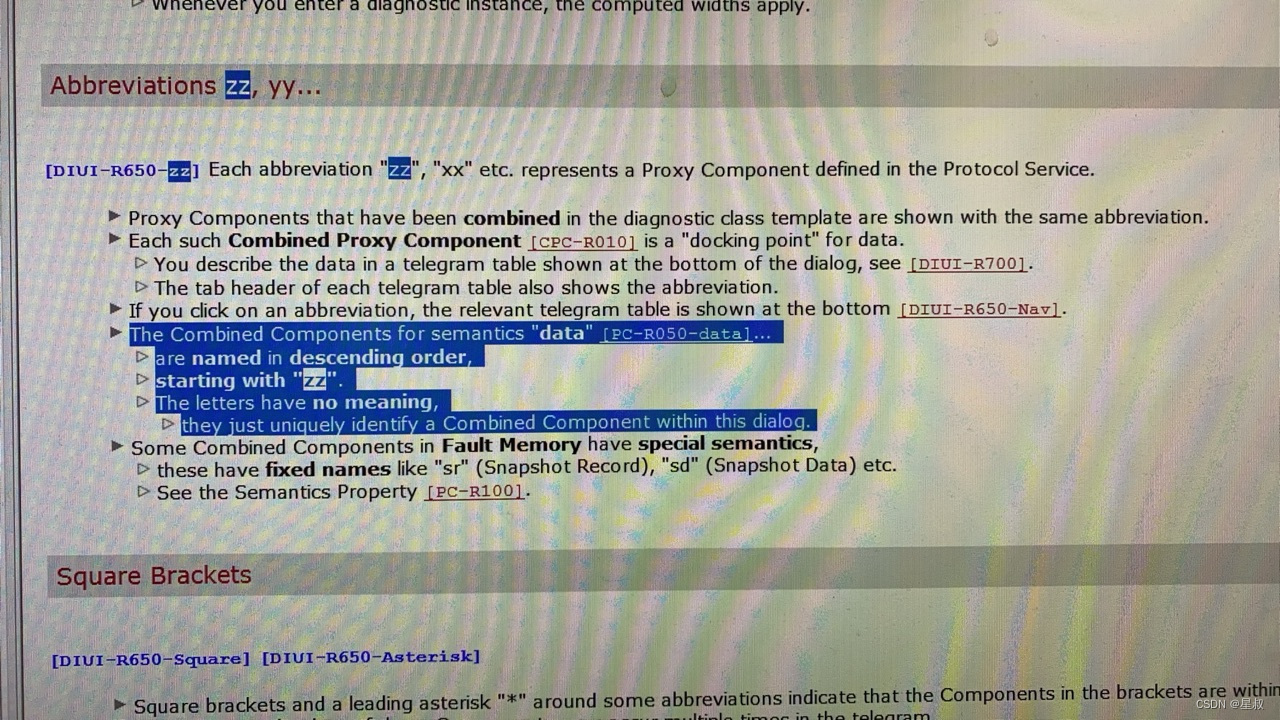
Cdd诊断数据控中的zz rc yy
如上图所示的Cdd Candela Diagnostic Descriptions 诊断数据库会话定义中有许多的标识符缩写,如zz rc LL xx 等 其实这些字母没有意义,它们只是唯一地标识对话框中的组合组件。
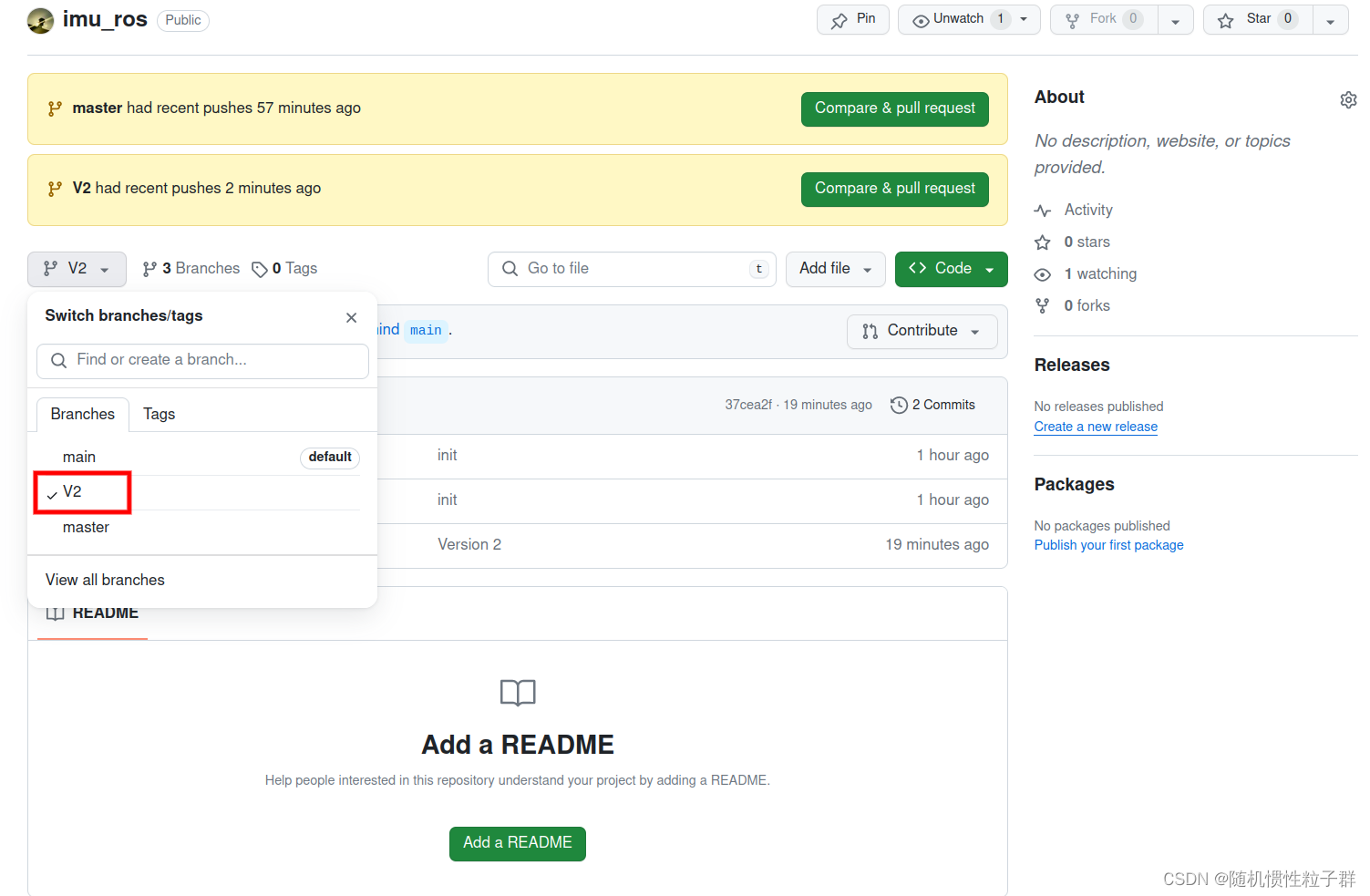
Github上传代码/删除仓库/新建分支的操作流程记录
首先先安装git,安装完git后,看如下操作指令:
输入自己的用户名和邮箱(为注册GITHUB账号时的用户名和邮箱): git config --global user.name "HJX-exoskeleton" git config --global user.email …
Mysql事务的处理
1、事务,就是一组命令的操作。 不过这一组命令,我们有时候需要使用手动提交; 1、使用这组命令可以查询出来现在的提交方式:自动提交(就是命令输入,点击enter后,会不会直接对表格产生修改&#x…
深入理解Spring IOC
1. IOC 理论
IOC 全称控制反转,英文名为 Inversion of Control,它还有一个别名为 DI(Dependency Injection),即依赖注入。
在我们刚接触Spring的时候,我们就听说了IOC,但是对于IOC的理解,貌似…
对快速排序思想的进一步理解,分而治之,欧几里得算法(常用求最大公约数的方法)
自己找到的最优的快排的代码
快速排序 思想 分而治之使用欧几里得算法(辗转相除法)来求解一个应用题 假设有一块地,现在用这个同样大小的正方形来铺满,求所可用的最大的正方形地砖的面积 这两个方法放在一起是因为这个欧几里得要…
Spring Security入门
目录
1.简介
与shiro对比
添加依赖
执行流程
2.UserDetailsService
User实现类
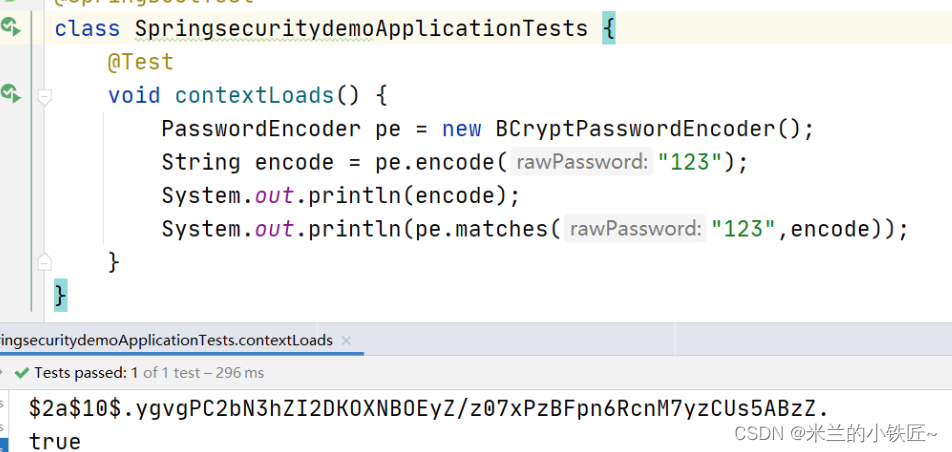
3.PasswordEncoder
BCryptPasswordEncoder
4.自定义登录逻辑
5.自定义登录界面
6.设置请求账户和密码的参数
7.自定义登陆处理器
成功
失败
8.判断
权限判断
角色判断
…
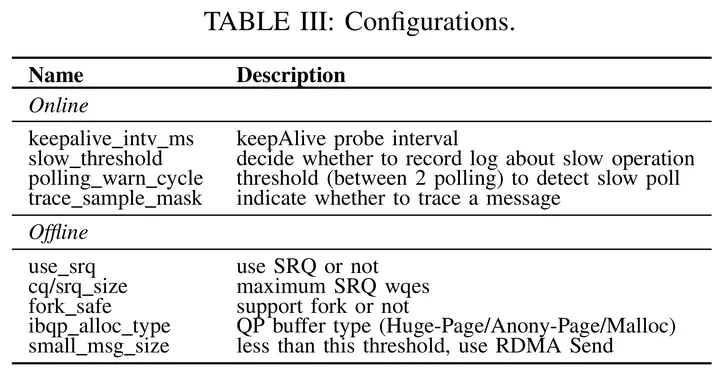
阿里云RDMA通信库XRDMA论文详解
RDMA(remote direct memory access)即远端直接内存访问,是一种高性能网络通信技术,具有高带宽、低延迟、无CPU消耗等优点。RDMA相比TCP在性能方面有明显的优势,但在编程复杂度上RDMA verbs却比TCP socket复杂一个数量级。
开源社区和各大云厂…
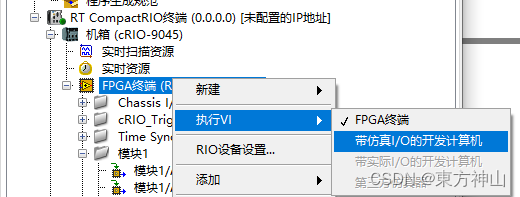
【LabVIEW FPGA入门】没有CompactRIO时进行编程测试
1.新建一个空白项目。 2.新建cRIO终端。 要添加仿真的远程实时目标,请选择项目名称,右击并选择新建>>目标和设备(Targets and Devices)。 3.新建终端和设备,选一个cRIO型号 接下来,当添加目标和设备窗口出现时,请…
Gauss消去法(C++)
文章目录 算法描述顺序Gauss消去法列选主元Gauss消去法全选主元Gauss消去法Gauss-Jordan消去法 算法实现顺序Gauss消去法列选主元Gauss消去法全选主元Gauss消去法列选主元Gauss-Jordan消去法 实例分析 Gauss消去法是求解线性方程组较为有效的方法, 它主要包括两个操作, 即消元和…