本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/350557.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
Qt|大小端数据转换(补充)
Qt|大小端数据转换-CSDN博客
之前这篇文章大小端数据转换如果是小数就会有问题。
第一个方法: template <typename T>
static QByteArray toData(const T &value, bool isLittle) {QByteArray data;for (int i 0; i < sizeof(T); i) {int bitOffset…
js 多对象去重(多属性去重)
需求中发现后端可能没有处理重复数据,这个时候前段可以直接解决。
在 JavaScript 中,可以使用 Set 数据结构来进行多对象的去重。Set 是 ES6 新引入的集合类型,其特点是元素不会重复且无序。
下面是一个示例代码,展示如何通过 S…
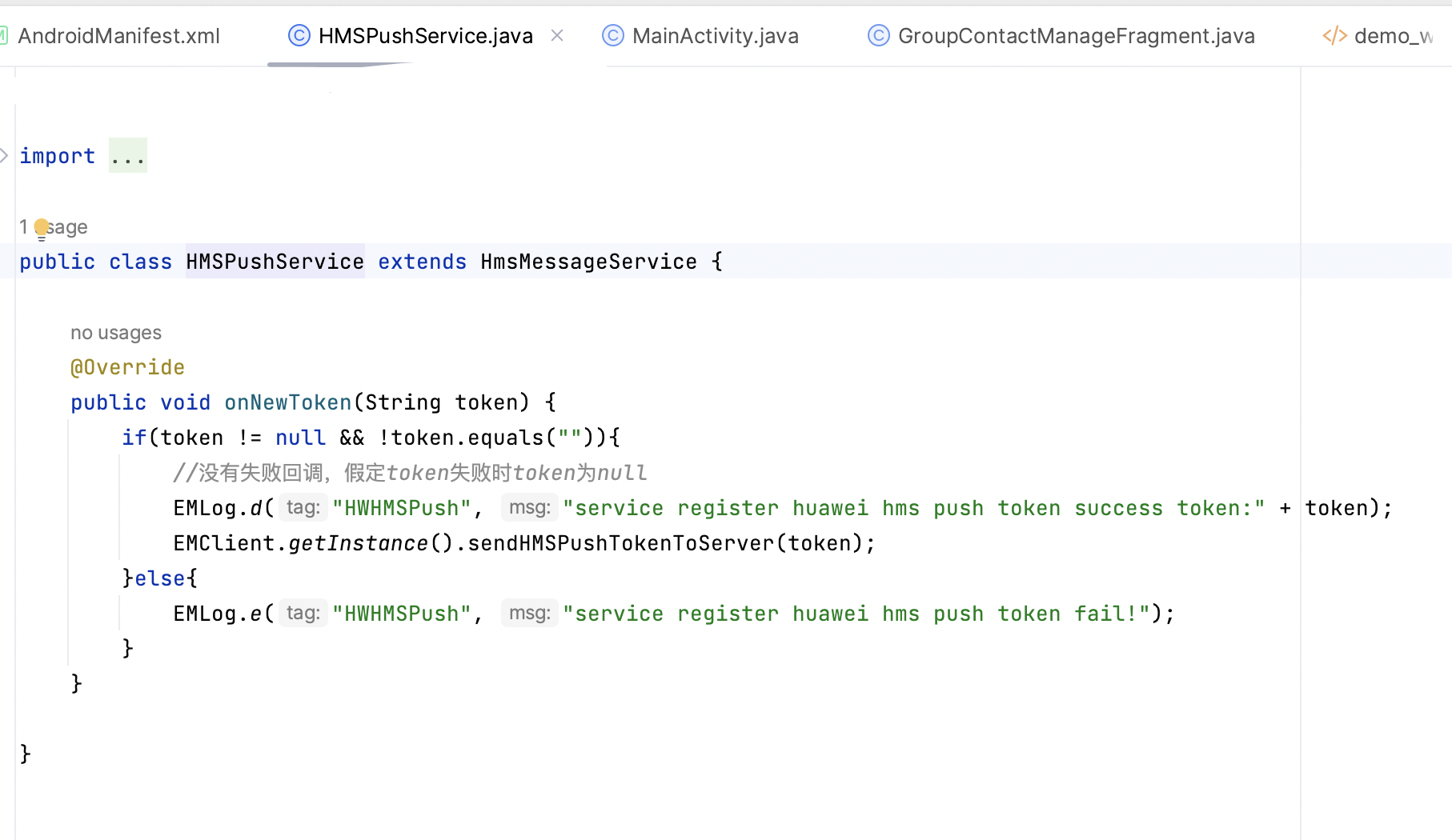
环信IM Android端实现华为推送详细步骤
首先我们要参照华为的官网去完成 ,以下两个配置都是华为文档为我们提供的
1.https://developer.huawei.com/consumer/cn/doc/HMSCore-Guides/android-config-agc-0000001050170137#section19884105518498
2.https://developer.huawei.com/consumer/cn/doc/HMSCore…
区块链之光:揭秘Web3时代的创新契机
随着技术的不断演进,区块链技术正逐渐引领着数字化时代的新潮流。Web3作为区块链技术的核心,为我们带来了前所未有的创新契机。本文将深入揭秘Web3时代的创新契机,探讨区块链之光如何改变我们的世界。 1. 区块链技术的兴起
区块链技术作为一…
electron Tab加载动画开启和关闭
记个开发中的bug,以此为鉴。眼懒得时候手勤快点儿,不要想当然!!!
没有转载的价值,请勿转载搬运呦。
WebContents API:
Event: did-finish-load
导航完成时触发,即选项卡的旋转…
逻辑回归为什么使用交叉熵而不用均方差?
逻辑回归为什么使用交叉熵而不用均方差?或者说逻辑回归的损失函数为什么不用最小二乘?
下面主要从两个角度进行阐述:
从逻辑回归的角度出发,逻辑回归的预测值是一个概率,而交叉熵又表示真实概率分布与预测概率分布的…
redis的搭建 RabbitMq搭建
官网
Download | Redis
wget https://github.com/redis/redis/archive/7.2.4.tar.gz 编译安装
yum install gcc g
tar -zxvf redis-7.2.4.tar.gz -C /usr/localcd /usr/local/redis make && make install 常见报错
zmalloc.h:50:10: fatal error: jemalloc/jemal…
PROBIS铂思金融破产后续:ASIC牌照已注销
2024年1月31日,PROBIS铂思金融的澳大利亚ASIC牌照 (AFSL 338241) 被注销《差价合约经纪商PROBIS宣布破产,澳大利亚金融服务牌照遭暂停》,这也就意味着,PROBIS铂思金融目前已经没有任何金融牌照。 值得注意的是,时至今日…
初识ONLYOFFICE 8.0:办公软件的革命性升级
引言
随着数字化时代的到来,办公软件已经成为我们日常生活和工作的重要组成部分。在这个充满竞争的市场中,ONLYOFFICE凭借其卓越的性能和功能,脱颖而出,成为许多企业和个人用户的优选。近期,ONLYOFFICE推出了全新的8.…
Java之获取Nginx代理之后的客户端IP
Java之获取Nginx代理之后的客户端IP
Nginx代理接口之后,后台获取的IP地址都是127.0.0.1,解决办法是需要配置Nginx搭配后台获取的方法,获得设备的真实地址。我们想要获取的就是nginx代理日志中的这个IP
nginx配置
首先在nginx代理的对应lo…
【Flink】FlinkSQL读取hive数据(批量)
一、简介:
Hive在整个数仓中扮演了非常重要的一环,我们可以使用FlinkSQL实现对hive数据的读取,方便后续的操作,本次例子为Flink1.13.6版本
二、依赖jar包准备:
官网地址如下:
Overview | Apache Flink
1、我们需要准备相关的jar包到Flink安装目录的lib目录下,我们需…
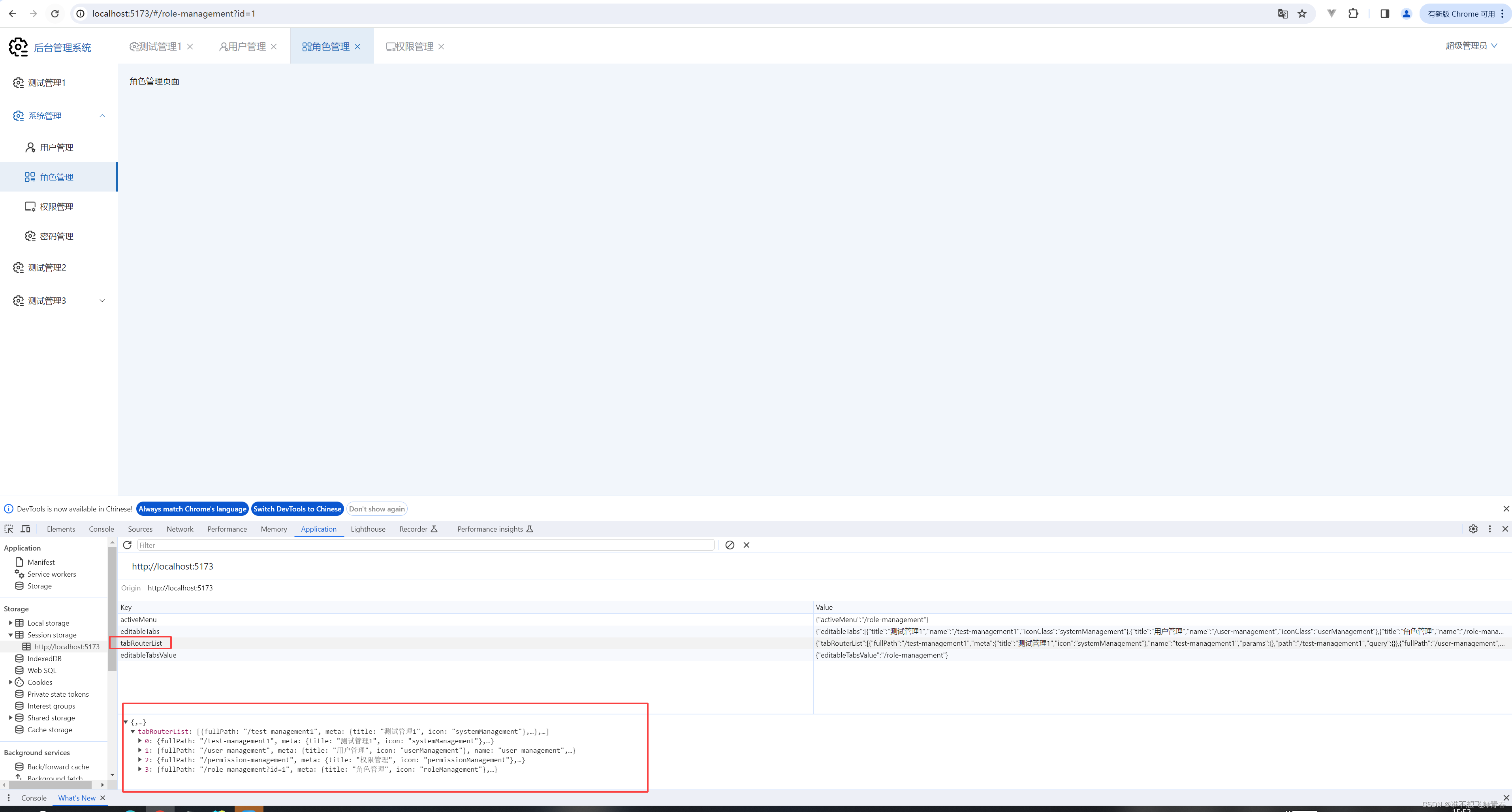
Vue3+vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现
Vue3vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现 说明删除项目中不需要的文件userStore全局属性代码菜单栏代码Tab页代码解决浏览器输入地址时不会打开tab页问题和切换tab页时参数丢失问题 说明
这里记录下自己在Vue3vite的项目使用less来写样式…
python3+requests+unittest:接口自动化测试(一)
简单介绍框架的实现逻辑,参考代码的git地址:
GitHub - zhangying123456/python_unittest_interface: pythonunittest接口自动化测试脚本
1.环境准备
python3 pycharm编辑器
2.框架目录展示
(该套代码只是简单入门,有兴趣的可…
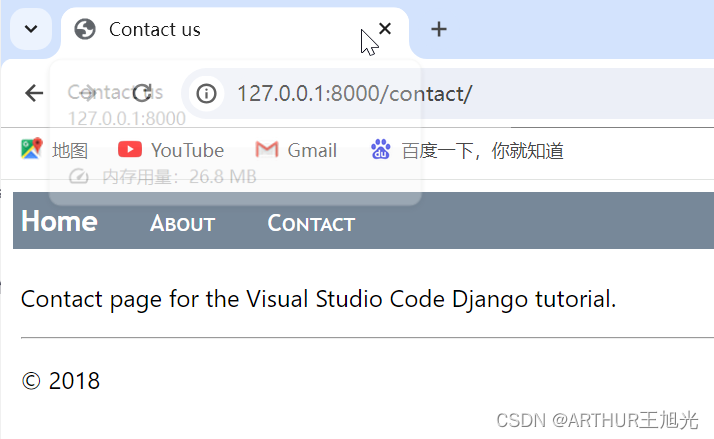
VSCODE使用Django 页面和渲染
https://code.visualstudio.com/docs/python/tutorial-django#_use-a-template-to-render-a-page 通过模板渲染页面 文件
实现步骤
1, 修改代码,hello的App名字增加到installed_apps表中。 2, hello子目录下,创建 .\templates\…
WSL里的Ubuntu 登录密码忘了怎么更改
环境:
Win10 专业版
WSL2 如何
Ubuntu22.04
问题描述:
WSL里的Ubuntu 登录密码忘了怎么更改
解决方案:
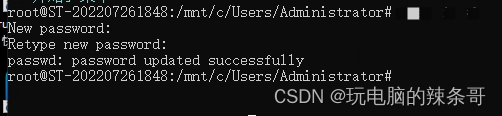
在WSL中的Ubuntu系统中,忘记了密码,可以通过以下步骤重置密码:
1.打开命令提示符或PowerShel…
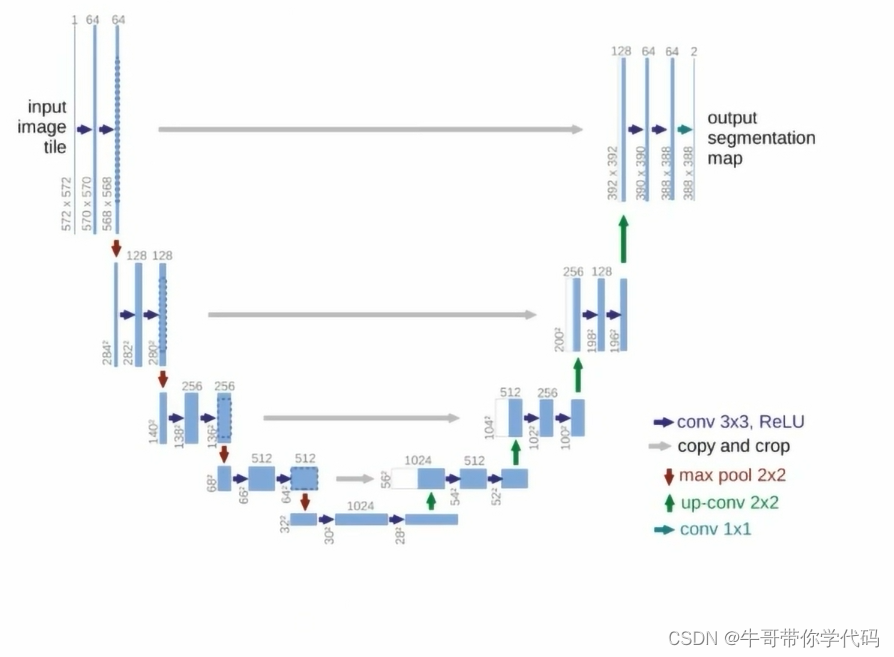
深度学习基础——U-Net图像分割
图像分割,就是根据图像的某种相似性特征(如亮度、颜色、纹理、面积、形状、位置、局部统计特征或频谱特征等)将医学图像划分为若干个互不相交的“连通”区域。 相关特征在同一区域内表现出一致性或相似性,而在不同区域间表现出明显的…
【k近邻】 K-Nearest Neighbors算法原理及流程
【k近邻】 K-Nearest Neighbors算法原理及流程 【k近邻】 K-Nearest Neighbors算法距离度量选择与数据维度归一化 k近邻算法(K-Nearest Neighbors,简称KNN)是一种常用的监督学习算法,可以用于分类和回归问题。在OpenCV中ÿ…
视频接入协议之MIPI
MIPI(Mobile Industry Processor Interface)是一种用于移动设备的串行接口标准,旨在提供高速、低功耗、低成本的接口解决方案。MIPI联盟是一个全球性的组织,致力于开发、推广和管理MIPI标准。
MIPI接口包括了多种协议和规范&…
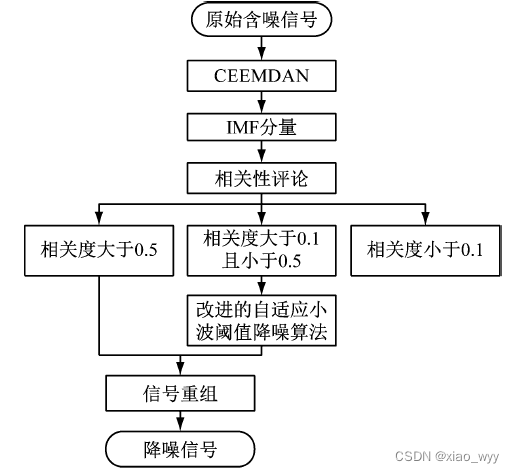
《基于CEEMDAN-IAWT 方法的滚动轴承振动信号降噪》算法思路笔记
思路:借鉴其在最优小波基、分解层数的应用 [1]任海军,韦冲,谭志强等.基于CEEMDAN-IAWT方法的滚动轴承振动信号降噪[J].振动与冲击,2023,42(13):199-207268.DOI:10.13465/j.cnki.jvs.2023.13.024.
CEEMDAN不再介绍 他这个改进的IAWT有两个创新,第一&…
力扣773. 滑动谜题(BFS)
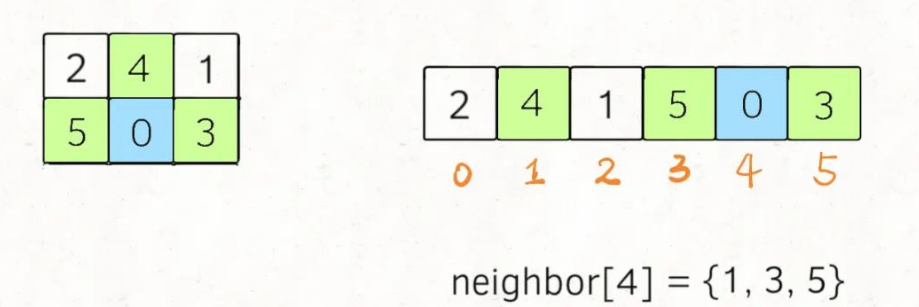
Problem: 773. 滑动谜题 文章目录 题目描述思路解题方法复杂度Code 题目描述 思路
由于题目提到最小步数,则可以使用BFS来穷举出最小的结果 1.转换为BFS问题:由于0代表空着的可以移动的位置,所以我们只需要从当前位置和0的相邻位置移动从而转…