本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/432195.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
计算机Java项目|基于SpringBoot的医疗报销系统的设计与实现
作者主页:编程指南针 作者简介:Java领域优质创作者、CSDN博客专家 、CSDN内容合伙人、掘金特邀作者、阿里云博客专家、51CTO特邀作者、多年架构师设计经验、多年校企合作经验,被多个学校常年聘为校外企业导师,指导学生毕业设计并参…
qtsql连接达梦数据库
odbc
window和linux都有odbc的中间件,可以通过odbc中间件配合qtsql连接数据库
windows下配置odbc linux配置odbc apt install unixodbc unixodbc-dev /etc/odbcinst.ini配置
[DM8 ODBC DRIVER]
DescriptionDM8 ODBC Driver
DRIVER/opt/dmdbms/bin/libdodbc.so/et…
eNSP 华为远程访问路由器
华为远程访问路由器 前提:主机能与路由器通信就行,如果不同网段就配路由协议,这里直接模拟直连通信
Cloud: R:
<Huawei>sys
[Huawei]sys R
[R]int g0/0/0
[R-GigabitEthernet0/0/0]
[R-GigabitEthernet0/0/0]…
WMS与ERP系统的区别是什么?
WMS(仓库管理系统)和ERP(企业资源计划)系统是两种不同类型的管理软件,它们各自有不同的功能和应用场景。以下是它们的主要区别:
——————————————————
1、功能范围: 1):WMS&a…
Centos7 message日志因dockerd、kubelet、warpdrive、containerd等应用迅速增长
问题:公司服务器在部署一套业务后,message日志记录大量的dockerd、kubelet、warpdrive、containerd应用日志,每天增加2G大小的日志 解决方案:
前期吐槽下:发现某个帖子,需要会员或者花钱才能看,…
bbr 多流共存的动态行为
若要更加全面展示多流共存场景的动态,需更新了一下仿真函数,模拟新流侵入和退出场景:
void simulate_one_phase(int i)
{double rtt;bbr_update_sending_bw(&f1);bbr_update_sending_bw(&f2);bbr_update_sending_bw(&f3);bbr_up…
<数据集>红绿灯识别数据集<目标检测>
数据集格式:VOCYOLO格式
图片数量:7884张
标注数量(xml文件个数):7884
标注数量(txt文件个数):7884
标注类别数:3
标注类别名称:[light_green, light_red, light_yellow]
序号类别名称图片数框数1lig…
利用Matlab求解高阶微分方程(ode45)
1、高阶微分方程的基本概念 二阶以及二阶以上的微分方程称之为高阶微分方程,一般来说,微分方程的阶数越高,求解的难度也就越大。求高阶方程的一个常用方法就是降低阶数。对二阶方程 ,如果能用变量代换把它化成一阶方程,…
设计模式-创建型模式-建造者模式
1.建造者模式定义 建造者模式又称生成器模式,将一个复杂对象的构建与表示分离,使得同样的构建过程可以创建不同的表示;
1.1 建造者模式优缺点
优点
封装性好,主要的业务员逻辑封装在指挥者类中;客户端不必知道产品内…
上位机图像处理和嵌入式模块部署(linux程序加解密)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 我们平时在开发程序的时候,如果仅仅是自己使用,那么代码和使用场景都是自己控制的,一般来说问题不大。但是程序…
PX4固定翼控制器详解(四)——TECS高度、速度控制器(续)
回顾复习
上一期关于TECS控制器的讲解,我们得到了基础框架下的TECS控制器如下图所示。
总能量、比能量相关量计算方式如下: { E ˙ V ˙ g γ B ˙ γ − V ˙ g E ˙ e ( V ˙ s p g γ s p ) − ( V ˙ g γ ) B ˙ e ( γ s p − V ˙ s p…
详细说明:向量数据库Faiss的搭建与使用
当然,Faiss(Facebook AI Similarity Search)是一个用来高效地进行相似性搜索和密集向量聚类的库。它能够处理大型数据集,并且在GPU上的性能表现尤为出色。下面详细介绍Faiss的搭建与使用。
1. 搭建Faiss
1.1 安装依赖包
首先&a…
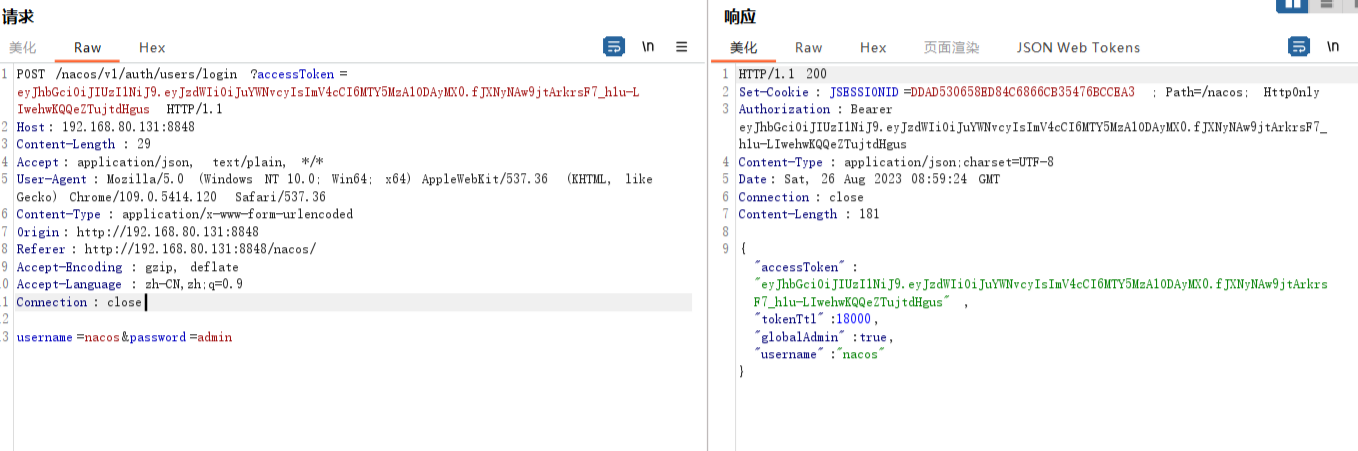
Nacos漏洞检测总结
弱口令
默认账号密码
nacos/nacos
POST /nacos/v1/auth/users/login HTTP/1.1
Host: xxxx:8848
Connection: keep-alive
Content-Length: 29
Accept: application/json, text/plain, */*
User-Agent: Mozilla/5.0 (Windows NT 10.0; WOW64) AppleWebKit/537.36 (KHTML, like…
HanLP分词的使用与注意事项
1 概述
HanLP是一个自然语言处理工具包,它提供的主要功能如下:
分词转化为拼音繁转简、简转繁提取关键词提取短语提取词语自动摘要依存文法分析
下面将介绍其分词功能的使用。 2 依赖
下面是依赖的jar包。
<dependency><groupId>com.ha…
ESP RainMaker OTA 自动签名功能的安全启动
【如果您之前有关注乐鑫的博客和新闻,那么应该对 ESP RainMaker 及其各项功能有所了解。如果不曾关注,建议先查看相关信息,知晓本文背景。】 在物联网系统的建构中,安全性是一项核心要素。乐鑫科技对系统安全给予了极高的重视。ES…
虚幻5|AI行为树,跟随task(非行为树AI)
这个可以不需要行为树
1.打开ai的角色蓝图后,添加一个函数,命名为跟距离改变速度
并用tick调用 2.编辑函数
并发系统的 CSP+PAT 形式化建模与验证方法(以Kafka系统为例)
消息队列中间件是分布式系统的重要组成部分。它允许应用程序仅关注数据本身,而无需关心数据传输的具体细节。这一特性有效解决了消息异步传输、应用程序解耦以及流量削峰等问题。Kafka是一个开源的分布式消息系统,它基于发布-订阅模型构建。Kafka具有低延…
【html+css 绚丽Loading】 - 000009 五行逆流珠
前言:哈喽,大家好,今天给大家分享htmlcss 绚丽Loading!并提供具体代码帮助大家深入理解,彻底掌握!创作不易,如果能帮助到大家或者给大家一些灵感和启发,欢迎收藏关注哦 💕…
利用Matlab求解常微分方程(dsolve与ode45)
1.微分方程的基本概念
含义微分方程(英语:Differential equation,DE)是一种数学方程,用来描述某一类函数与其导数之间的关系。微分方程的通解是一个符合方程的函数。而在初等数学的代数方程里,解析解是一个…
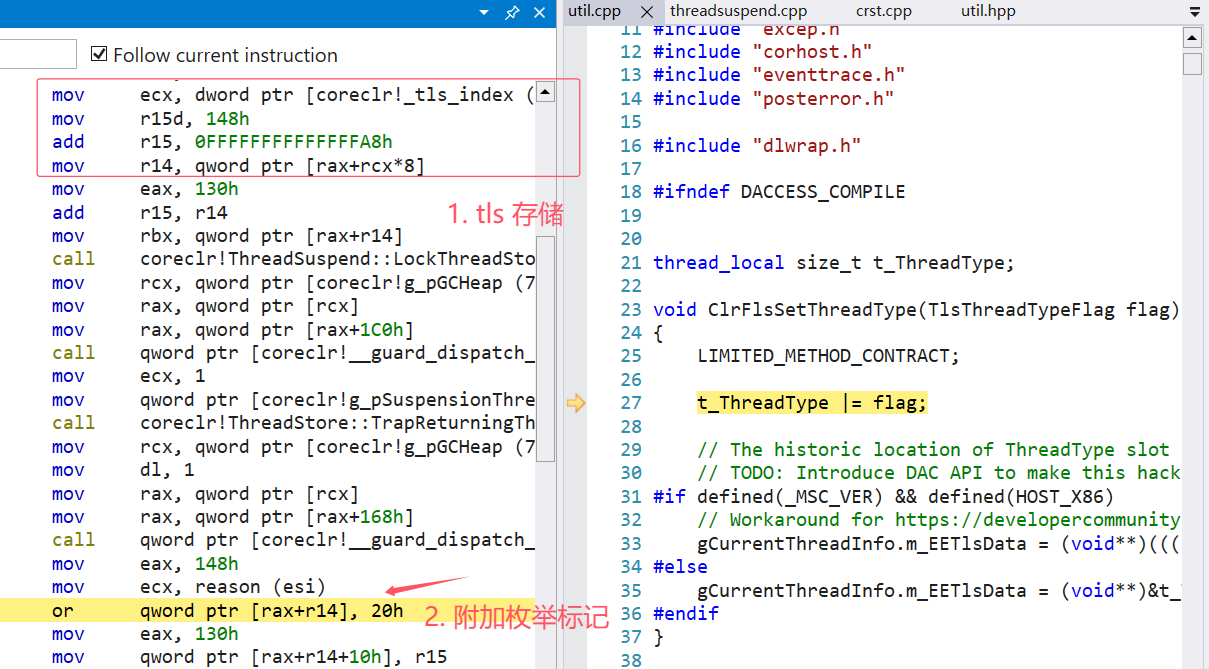
GC终结标记 SuspendEE 是怎么回事
一:背景
1. 讲故事
写这篇是起源于训练营里有位朋友提到了一个问题,在 !t -special 输出中有一个 SuspendEE 字样,这个字样在 coreclr 中怎么弄的?输出如下: 0:000> !t -special
ThreadCount: 3
UnstartedTh…