本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.ldbm.cn/p/449095.html
如若内容造成侵权/违法违规/事实不符,请联系编程新知网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
网盘能否作为FTP替代产品?企业该如何进行FTP国产化替代?
近年来,信创的概念引入和高效实践落地让更多的行业企业自发性地进行国产化替代,目前信创国产化替代还多发生在操作系统和应用层面,软件工具等目前还在下一阶段规划,但很多企业未雨绸缪,已经在做调研和尝试。 FTP作为世…
Skywalking告警配置
背景 skywalking 9.7.0,地址:Backend setup | Apache SkyWalking helm:skywalking-helm:4.5.0,地址:skywalking-helm/chart/skywalking/values.yaml at v4.5.0
首先来说一下为什么使用skywalking告警?
…
Linux驱动开发(速记版)--平台总线
第四十七章 平台总线模型介绍
47.1 什么是平台总线? 平台总线是Linux内核中的一种虚拟机制,用于连接和匹配平台设备与对应的平台驱动。它简化了设备与驱动之间的绑定过程,提高了系统对硬件的适配性和扩展性。 当设备或驱动被注册时ÿ…
解决麒麟操作系统自定义数据盘/data在图形界面不显示盘符的问题
解决麒麟操作系统自定义数据盘/data在图形界面不显示盘符的问题 1、问题描述2、问题分析3、问题解决办法 💖The Begin💖点点关注,收藏不迷路💖 1、问题描述
在系统自定义安装过程中,用户可能会根据需要设置多个分区&a…
微信小程序开发之多图片上传+.NET WebAPI后端服务保存图片资源
前言: 最近开发的一个微信小程序项目需要做一个同时选中三张(或者是多张)图片一起上传到服务端,服务端保存图片资源并保存的功能。发现在微信小程序开发中会有很多场景会使用到多图片上传并保存到的功能,所以我把自己总…
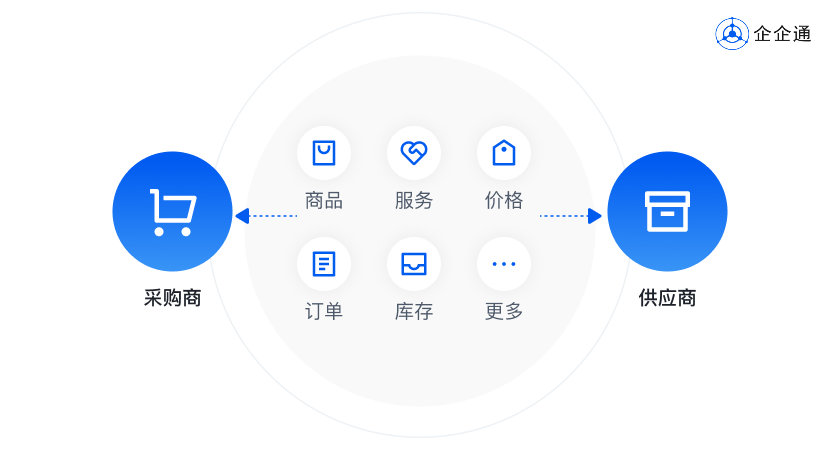
B2B商城交易解决方案:赋能企业有效重塑采购与销售新生态
在电商零售领域,商城系统始终是企业搭建商城的关键利器。 伴随着电商行业的蓬勃发展,各类新模式层出不穷,各种商城系统也应运而生,其中B2B商城更是最为常见的一种。 近年来,得益于电子商务的迅猛发展,B2B商…
埃及 Explained
古埃及,位于尼罗河畔的神秘文明,曾在北非的荒漠中繁荣昌盛。这个充满谜团的王国凭借其宏伟的成就和神秘的文化,数百年来吸引了无数人的好奇心。
埃及人创造了复杂的象形文字,建造了像吉萨大金字塔这样宏伟的建筑,并通…
鸿蒙harmonyos next纯flutter开发环境搭建
公司app是用纯flutter开发的,目前支持android和iOS,后续估计也会支持鸿蒙harmonyos。目前谷歌flutter并没有支持咱们国产手机操作系统鸿蒙harmonyos,于是乎国内有个叫OpenHarmony-SIG的组织,去做了鸿蒙harmonyos适配flutter开发的…
【数学分析笔记】第4章第2节 导数的意义和性质(2)
4. 微分
4.2 导数的意义与性质
4.2.3 单侧导数 f ′ ( x ) lim Δ x → 0 f ( x Δ x ) − f ( x ) Δ x lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f(x)\lim\limits_{\Delta x\to 0}\frac{f(x\Delta x)-f(x)}{\Delta x}\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)…
TI DSP TMS320F280025 Note16:EPWM的原理与使用
TMS320F280025 模数转换器(ADC) ` 文章目录 TMS320F280025 模数转换器(ADC)时基TB子模块计数比较CC子模块动作AQ子模块死区DB子模块斩波PC子模块错误联防模块TZ子模块数字比较DC子模块中断ET子模块EPWM的使用EPWMDriver.cEPWMDriver.h每个EPWM模块都包含多个子模块:时基TB子模…
全新一区PID搜索算法+TCN-LSTM+注意力机制!PSA-TCN-LSTM-Attention多变量时间序列预测(Matlab)
全新一区PID搜索算法TCN-LSTM注意力机制!PSA-TCN-LSTM-Attention多变量时间序列预测(Matlab) 目录 全新一区PID搜索算法TCN-LSTM注意力机制!PSA-TCN-LSTM-Attention多变量时间序列预测(Matlab)效果一览基本…
解决 Android WebView 无法加载 H5 页面常见问题的实用指南
目录
1. WebView 简介
2. 常见问题
3. 网络权限设置
4. 启用 JavaScript
5. DOM Storage 的重要性
6. 处理 HTTPS 问题
7. 设置 WebViewClient
8. 调试工具
9. 其他调试技巧
10. 结论
相关推荐 1. WebView 简介 Android WebView 是一种视图组件,使得 And…
基于SSM+小程序的电影院订票选座管理系统(电影2)(源码+sql脚本+视频导入教程+文档)
👉文末查看项目功能视频演示获取源码sql脚本视频导入教程视频
1、项目介绍
基于SSM的电影院订票选座小程序管理系统实现了管理员和用户二个角色。管理员实现了用户管理、影院信息管理、电影类型管理、电影信息管理、系统管理、订单管理等。用户实现了影院信息、电…
Figma:现代设计工具使用指南
Figma:现代设计工具使用指南 在当今数字设计的世界中,Figma 已经成为设计师、开发者和团队协作的重要工具。作为一款基于云的设计平台,Figma 不仅支持界面设计和原型制作,还提供强大的协作功能。本文将详细介绍 Figma 的主要功能、…
LeetCode 面试经典150题 50.Pow(x,n)
题目:实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即, )。
思路: 代码:
class Solution {public double myPow(double x, int n) {double ans 1;long N n;if (N < 0) {N -N;x 1 / x;}…
Linux工具的使用——yum和vim的理解和使用
目录 linux工具的使用1.linux软件包管理器yum1.1yum的背景了解关于yum的拓展 1.2yum的使用 2.Linux编辑器-vim使用2.1vim的基本概念2.2vim的基本操作2.3命令模式命令集2.3.1关于光标的命令:2.3.2关于复制粘贴的命令2.3.3关于删除的命令2.3.4关于文本编辑的命令 2.4插…
腾讯一面-LRU缓存
为了设计一个满足LRU(最近最少使用)缓存约束的数据结构,我们可以使用哈希表(HashMap)来存储键值对,以便在O(1)时间复杂度内访问任意键。同时,我们还需要一个双向链表(Doubly Linked …
Golang | Leetcode Golang题解之第448题找到所有数组中消失的数字
题目: 题解:
func findDisappearedNumbers(nums []int) (ans []int) {n : len(nums)for _, v : range nums {v (v - 1) % nnums[v] n}for i, v : range nums {if v < n {ans append(ans, i1)}}return
}
【人人保-注册安全分析报告-无验证方式导致安全隐患】
前言
由于网站注册入口容易被黑客攻击,存在如下安全问题:
1. 暴力破解密码,造成用户信息泄露
2. 短信盗刷的安全问题,影响业务及导致用户投诉
3. 带来经济损失,尤其是后付费客户,风险巨大,造…